第一次练习课

准备工作

  1. 各自携带笔记本电脑，并预先安装好 R 和 RStudio。

  2. 针对前三次课讲授的内容进行练习。

  3. 熟悉使用脚本（script）模式编辑并运行程序。

脚本模式

从菜单栏选择 File > New File > R Script 即可打开脚本编辑窗口，如下图左上部份。

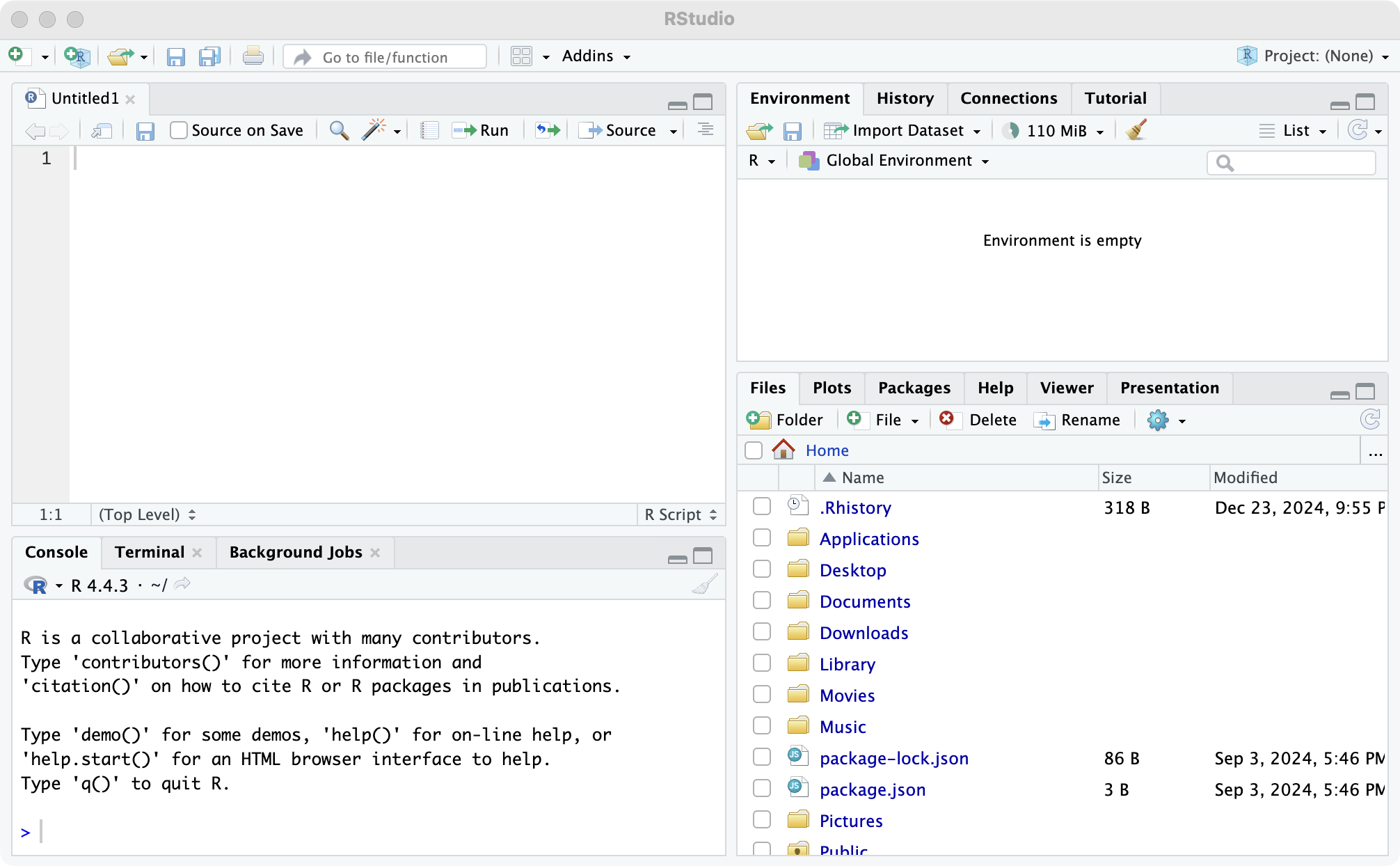RStudio 中的脚本编辑窗口（左上） 像编辑任何类型的文本文件一样，在此窗口中编辑的内容可以以文件的形式保存在电脑中。点击 File > Save 或磁盘图标即可保存。R 脚本文件的扩展名是 “.R”。

在脚本中，换行并不会执行该行程序。执行脚本程序有通常两种方法：

  1. 执行光标所在行，或者选中的部份（如下图），可以点击窗口上方的 “Run” 键，或使用快捷键 Ctrl/Cmd + ⏎。

  2. 执行整个文件，可以点击窗口上方的 “Source” 键，或使用快捷键 Ctrl/Cmd + Shift + S 或 Ctrl/Cmd + Shift + ⏎。两者的区别是后者会在 Console 中显示所有的代码和结果，而前者则都在后台执行并忽略显示变量内容的命令（如下图中第 6 行）

运行脚本中的程序

运行脚本中的程序

更多信息可参考 R for Data Science (2e), Chapter 6. Workflow: scripts and projects 。

练习内容

第一题

首先运行下面的程序

set.seed(111)
x <- rnorm(20, mean = 5, sd = 0.5) |> round(digits = 1)

第一行 set.seed(111) 是给第二行的 rnorm() 函数做准备，目的是保证大家都能生成同样的结果。确保第一行运行后再运行第二行。

回答下面的问题：

  1. 描述第二行程序 x <- rnorm(20, mean = 5, sd = 0.5) |> round(digits = 1) 的作用。

  2. 依次完成下列计算。如果不知道用什么函数，可利用参考书或网络搜索进行学习。

    (i). 将 x 中的值从小到大排序后代入变量 y。

    (ii). 将 y 中的值标准化，即 (y_i - \hat{\mu}_y) / \hat{\sigma}_y，然后代入变量 y_stand。

    (iii). 计算 y_stand 的经验分布函数（ECDF）值，即 F(t) = \#\{y_{i,\mathrm{stand}} \leq t \} / n，并保存至变量 y_psample。注意 y_psample 的长度应和 y_stand 一致。ecdf() 函数无法给出符合条件的结果，需利用 for 命令进行循环计算。可参考 A (very) short introduction to R 中的第 11.2 节。

    (iv). 计算 y_stand 对应的正态分布函数值，并保存至变量 y_pnorm。

    (v). 计算 y_psample 和 y_pnorm 之间的均方误差（mean squared error, MSE），即 \sum(y_{i,\mathrm{ps}} - y_{i,\mathrm{pn}})^2 / n。

  3. 利用 x 中的数据检验假设 H_0: \overline{X} = 5。可以使用 t.test() 函数。p-值等于多少？你的结论是什么？给出 95% 置信区间。

第二题

调入 tidyverse 包，并回答下面的问题：

  1. 了解数据集 women，它是什么类型的数据？

  2. 将 women 转为 tibble 数据并代入变量 women_tb。

  3. 在 women_tb 中添加新的一列，名称为 bmi，根据已有数据计算该列数值并存入。注意原有数据的单位。此操作可以用一行命令完成。

  4. 针对身高 height 小于 66 的观测值，计算体重 weight 和BMI bmi 的均值。

作业

完成上面的练习，将答案（包括对问题的回答，以及对应的 R 程序及其运行结果）整理为 PDF 文件，通过教学平台提交。

截止日期：2025年3月27日（星期四）23:00

参考答案