1 绪论

入门博弈论最好的方式是先了解一些例子。在这一章中，我们首先给出博弈论的通用定义，然后介绍一些历史，并介绍几个常用的例子，最后我们将简单讨论非合作博弈和合作博弈的区别。

1.1 定义

博弈论（game theory）是一门利用数学方法研究多个参与人间的竞争与合作的学科。这个定义虽然很宽泛，但是很契合博弈论所覆盖的众多应用问题。从战争策略到市场竞争，从经济和社会上的公正分配问题到物种间的生存竞争，从桌游到政治选举等都是博弈论的研究对象。

虽然博弈论是美国经济学会官方公布的数学学科之一¹，但主要是经济学家在研究和应用它。在经济学领域，许多关于博弈论及其应用的论文和书籍都标注了美国经济学会的 JEL² 分类符号 C7x.

¹ AMS Classification code 90D.

² Journal of Economic Literature.

1.2 一些历史

本节请参考原书。

1.3 例子

本节中的每个例子都伴随着一个故事。每个例子都以故事开始，之后再被翻译成正式的数学模型。数学模型是故事的另一种描述方式，它刻画了故事中的关键因素，同时省略了不重要的细节。换句话说，数学模型是对故事的抽象化。在确定模型后，我们会尝试对它进行求解：即对参与人的行动进行预测。博弈的解可能是规范性的（normative）也可能是描述性的（positive），或者介于两者之间，但更多时候这类话题会留给读者思考。一般来说，最优化理论和博弈论之间的区别在于，前者的最优解通常是没有争议的，而后者因为研究对象是人（或更广泛的生物）的行为，对什么是最优行动往往存在争议，甚至对最优意味着什么也并没有共识。

在每个例子的最后都有一小段评论，也可能包含对该博弈解法的预告。例子被分成五组，分别是零和博弈，非零和博弈，扩展式博弈，合作博弈和讨价还价博弈。

1.3.1 零和博弈

1.3.1.1 俾斯麦海海战（the battle of the Bismarck Sea）

故事：故事发生在1943年的南太平洋。日军需要将部队从拉包尔送往新几内亚的莱城，而盟军则想通过空袭运输舰的方式阻止他们。日军有两种运输路线可以选择，北线（需2天）和南线（需3天），而盟军则需要选择一条线路进行空袭。如果盟军选择了错误路线，还可以召回轰炸机并重新派遣至正确的路线，但是可以空袭的天数会因此减1。我们假设空袭天数为盟军的收益（payoff），其负数为日军的收益。

模型：俾斯麦海海战问题可以用下面的表格描述 \begin{align*} & \begin{matrix} \text{北} & \text{南} \end{matrix} \\ \begin{matrix} \text{北} \\ \text{南} \end{matrix} \ \Bigg( & \begin{matrix} \, 2 & \ \ \, 2 \, \\ \, 1 & \ \ \, 3 \, \end{matrix} \Bigg) \end{align*}

这个表格描述了一个二人博弈，参与人（player）为盟军和日军。每个参与人都有两个选项：每一行代表盟军的一个选项，每一列代表日军的一个选项。两人需要同时且独立地进行选择。表格中的数字是盟军的收益，例如左上的 2 代表当盟军和日军都选择北线的时候，盟军的收益是 2，日军的收益是 -2。我们习惯让表格中的数字代表参与人 2（列参与人, column player）支付给参与人 1（行参与人, row player）的“报酬”。这个博弈是一个零和博弈，因为双方的收益之和永远是零。

解：在这个例子中不难预测双方的行动选择。从表中可以看出，日军选择北线永远不会比选择南线更差。因为当盟军选择北线时，日军选择北线和南线的收益都是 -2。而当盟军选择南线时，日军选择北线的收益是 -1，大于选择南线的收益 -3。因此我们可以安全地预测日军会选择北线。而盟军也会进行同样的推理并得出日军将选择北线的预测，因此盟军应当也选择北线，这是对日军选择北线的最佳响应（best reply）。这个例子中南线是日军的劣势（dominated）选项，即无论对手如何选择，北线至少能带来和南线相同的收益，有时候还会更好。

如果换一个角度我们可以发现，(北，北) 的行动组合给盟军带来的收益 2 在列方向取最大值（2 \geq 1）并且在行方向取最小值（2 \leq 2）。矩阵中满足这种性质的要素称为鞍点（saddle point）。在鞍点上，没有参与人愿意单方面改变自己的选择（事实上这个行动组合是纳什均衡）。同时鞍点也是行参与人最大化自己的最小收益，列参与人最小化自己的最大支付的结果。这个收益 2 （由参与人 2 支付给参与人 1）称作此博弈的值（value）。

评论：这个例子中的博弈是二人零和有限选择博弈（two-person zero-sum game with finitely many choices），也称为矩阵博弈（matrix game），因为它可以用一个矩阵表达。我们将在 Chapter 2 中学习矩阵博弈。(北，北) 的行动组合是符合史实的。

Figure 1.1: 俾斯麦海海战中日军可选择的路线（图片引自 https://policonomics.com/battle-of-the-bismarck-sea/）

1.3.1.2 猜硬币（matching pennies）

故事：猜硬币游戏也是一个二人博弈，每个参与人手中有一枚硬币，两人需要同时展示硬币的一面。如果出现的面相同，则参与人 2 将硬币输给参与人 1；如果出现的面不同，则参与人 1 将硬币输给参与人 2。

模型：这也是一个零和博弈，可以用下面的收益矩阵表达， \begin{align*} & \begin{matrix} \ \text{正} & \ \text{反} \end{matrix} \\ \begin{matrix} \text{正} \\ \text{反} \end{matrix} \ \Bigg( & \begin{matrix} \, 1 & -1 \, \\ \, -1 & 1 \, \end{matrix} \Bigg) \end{align*}

解：在这个博弈中，任意一方的选项都没有绝对的优势或劣势，选择正面比选择反面好或者差取决于对方的选择。同时，这个矩阵中不存在鞍点（在行方向取最小值同时在列方向取最大值的要素）。因此，这个博弈没有看上去比较自然的解。解决问题的一个办法是允许参与人在多个选项间随机选择：参与人 1 以概率 p 选择正面，以概率 1-p 选择反面；参与人 2 以概率 q 选择正面，以概率 1-q 选择反面。由于博弈的设定是对称的，那么让我们首先尝试假设 p=0.5。此时参与人 1 的期望收益是

\frac{1}{2}\big[q\cdot 1 + (1-q)\cdot (-1)\big] + \frac{1}{2}\big[q\cdot (-1) + (1-q)\cdot 1\big] = 0

此式不依赖 q 的取值，因此当参与人 1 选择 p=0.5 时，他可以保证自己的期望收益是 0（当然，博弈的结果要么是 1 要么是 -1）。同样的，参与人 2 如果选择 q=0.5 也可以保证自己的期望收益是 0。这里的 0 期望收益起到一种类似鞍点的作用，因此我们定义此博弈的值为 0。

评论：随机选择行动通常称为混合策略（mixed strategy）。如何理解随机选择？一个常用的解释是其他参与人“认为”这个参与人会如何做出选择，学术术语称作信念（belief）³。

³ 另一种解释是当博弈重复进行时，选择特定选项的频率。

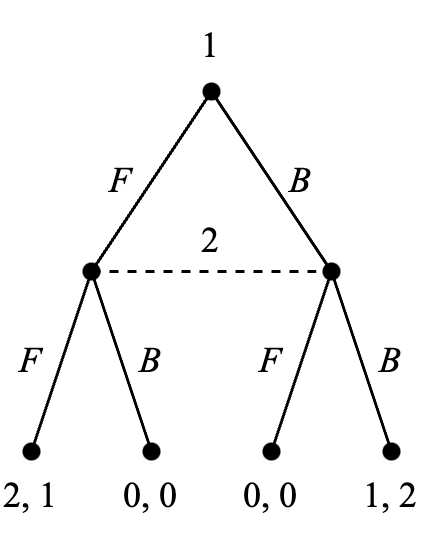
1.3.2 非零和博弈

1.3.2.1 囚徒困境（prisoner’s dilemma）

故事：两人因共同犯罪被捕，并且被分开审讯。每个罪犯有两种选择，一种是合作（cooperate, C），即和同伙串供，另一种是背叛（defect, D）并指证同伙的罪行。该罪行一旦确定需服刑10年，但需要有另一个人指证。在任何情况下选择背叛都会给自己减少1年刑期。如果自己没有被指证（即同伙没有背叛），则会因证据不足被判轻罪并服刑1年。

模型：这种情形可以总结为如下形式 \begin{align*} & \begin{matrix} \ \ \ \ \ C & \ \ \ \ \ \ \ \ \ \ D \end{matrix} \\ \begin{matrix} C \\ D \end{matrix} \ \Bigg( & \begin{matrix} \, -1, -1 & -10, 0 \, \\ \, 0, -10 & -9, -9 \, \end{matrix} \Bigg) \end{align*}

这个表格和前面的收益矩阵类似，区别是每个要素的位置有两个数字，分别是参与人 1（行）和参与人 2（列）的收益。此博弈不再是零和，所以我们需要明示双方各自的收益。

解：对于任意参与人，合作 C 都是严格劣势（strictly dominated）选项：因为无论对方选择什么，选择 D 都好过选择 C。因此，我们有理由认为此博弈的结果是双方选择 (D,D) 组合并获得收益 (-9, -9)。严格劣势策略的存在使囚徒困境博弈比较容易分析。

评论：收益 (-9, -9) 谈不上好，因为它不是帕累托最优（Pareto optimal），每个参与人都可以通过选择 C 来提升自己的收益至 -1。有大量文献讨论如何实现合作，例如通过重复博弈中的声誉效果。原书第七章讨论了重复博弈的相关内容。

囚徒困境用来比喻很多经济现象，其中一个很有名的例子是公地悲剧（tragedy of the common’s），见原书第六章的练习 6.27。

1.3.2.2 性别战（battle of the sexes）⁴

故事：一男一女打算晚上出去约会，两人可以选择去看足球赛或者芭蕾舞。但是他们忘记约定具体去干什么了，并且（因为某些原因）无法在出发前相互联系而只能各自决定自己的目的地。他们最希望能在一起，但除此之外，男人更喜欢看足球赛，女人则更喜欢看芭蕾舞。

模型：下面的表格提供了一种描述此情形的方式 \begin{align*} & \begin{matrix} \text{足球} & \text{芭蕾} \end{matrix} \\ \begin{matrix} \text{足球} \\ \text{芭蕾} \end{matrix} \ \Bigg( & \begin{matrix} \, \ 2, 1 & \ \ 0, 0 \, \\ \, \ 0, 0 & \ \ 1, 2 \, \end{matrix} \Bigg) \end{align*}

此时男人是行参与人，女人是列参与人。

解：首先，双方都没有劣势选项。这说明两人需要在没有沟通手段的情况下进行协作（coordinate）。或许在前一天晚上两人曾经花很长时间讨论过足球赛，而两人都记住了这件事，且相信对方也记住了这件事，因此这可能成为一个决定因素。在缺乏这类前提的情况下，我们很难预测双方会怎样选择。但是我们可以说 (足球，足球) 和 (芭蕾，芭蕾) 的组合具有独特的性质：这个时候双方的选择都是对方选择的最佳响应（best reply）。如果男人选择了足球（芭蕾），那么女人的最优选项也是足球（芭蕾），反之亦然。在博弈论中，这种互为最佳响应的选项组合被称为纳什均衡（Nash equilibrium）。纳什均衡毋庸置疑是最常用的博弈解。

评论：性别战博弈经常用来探讨协作问题。

⁴ 此处的中文翻译总觉得有些不地道，你能想到更好的翻译吗？

1.3.2.3 猜硬币

每个零和博弈都是非零和博弈的一种特殊形式，例如前面讨论过的猜硬币游戏就可以表达为 \begin{align*} & \begin{matrix} \ \ \ \text{正} & \ \ \ \ \ \ \ \text{反} \end{matrix} \\ \begin{matrix} \text{正} \\ \text{反} \end{matrix} \ \Bigg( & \begin{matrix} \, 1, -1 & \ -1, 1 \, \\ \, -1, 1 & \ 1, -1 \, \end{matrix} \Bigg) \end{align*}

可以明显的看出双方都没有劣势选项，也不存在纳什均衡。如果允许混合策略，则当参与人 2 以 0.5 的概率选择正面时，参与人 1 也应当以 0.5 的概率选择正面，反之亦然。这是混合策略纳什均衡，参照 Chapter 3。

1.3.2.4 古诺博弈（a Cournot game）

故事：有两家公司生产同一种产品。该产品的市场价格是 p= \max\{1-Q, 0\}，Q 是两家公司的总产量⁵。我们假设不存在生产成本。

模型：两家公司分别是参与人 1 和 2。参与人 i 选择自己的产量 q_i \geq 0，并获得利润

K_i(q_1, q_2) = q_i \max\{1-q_1 -q_2, 0\}

解：具有常识的参与人不会选择 q_i > 1。假设参与人 2 选择 q_2 = 1/3，则参与人 1 为了最大化自身利润 q_1(1-q_1 - 1/3) 会选择 q_1 = 1/3。反之，当参与人 1 选择 q_1 = 1/3 时，参与人 2 为了最大化自身利润 q_2(1 - 1/3 - q_2) 也会选择 q_2 = 1/3。这个策略组合 (q_1, q_2) = (1/3, 1/3) 互为最佳响应，因此是纳什均衡。

评论：这个纳什均衡也被称为古诺均衡（Cournot equilibrium）。注意在这个例子中古诺均衡也不是帕累托最优：如果两个公司都选择产量为 1/4，则双方都会获得更多利润（1/8 > 1/9）。这个例子和猜硬币游戏的主要区别是，在不考虑混合策略的情况下，这个例子中的参与人有无穷多个选项。参照 Chapter 6。

⁵ 在什么情况下这个假设是合理的？

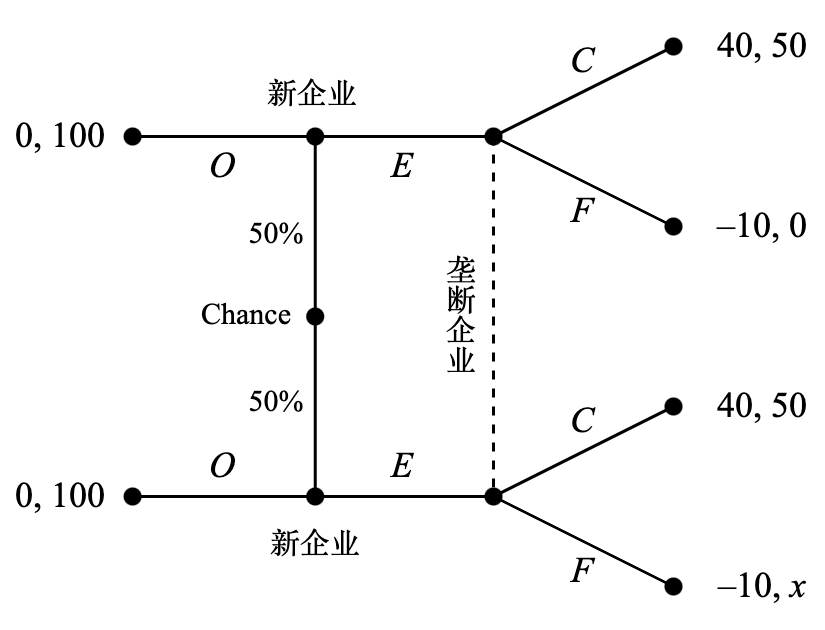
1.3.3 扩展式博弈

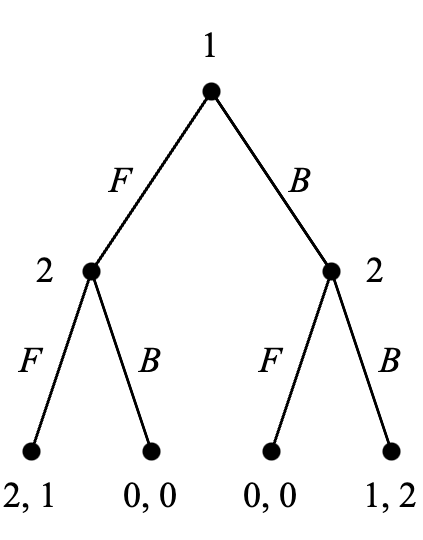
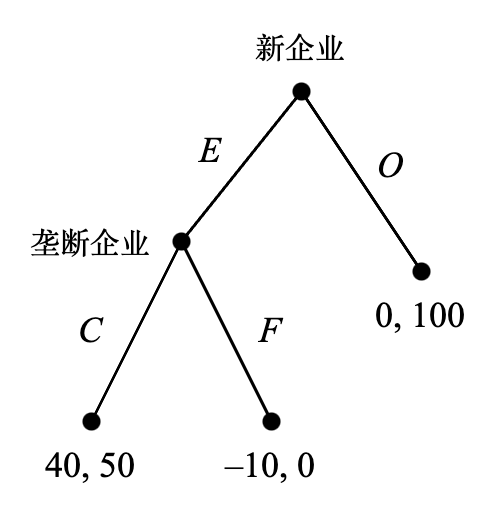
前面介绍的所有博弈都是单次（one-shot）博弈，即参与人只进行一次选择，且选择需要同时独立进行。所有的室内桌游，或者从现实的经济政治问题提炼出的博弈通常都不符合这一特征。参与人往往可以按一定顺序进行选择（称为序贯，sequentially），同时能够观察（或部分观察）对手的选择结果。这种情形可以用扩展式博弈（extensive form game）来建模。

1.3.3.1 序贯性别战（sequential battle of the sexes）

故事：和 Section 1.3.2 中性别战的例子类似，但这里我们令男人首先做出选择，女人可以观察到男人选择的结果。

模型：这种情况可以用 Figure 1.2 中的决策树描述。参与人 1（男人）首先进行选择，参与人 2（女人）在观察到参与人 1 的行动后选择自己的行动。最下面的节点（终点）下的两个数字中，第一个对应参与人 1 的收益，第二个对应参与人 2 的收益。非终点的节点对应一个参与人的决策。

解：此博弈的一个解法是利用逆向推理。如果参与人 1 选择了 F（即足球），则参与人 2 也应该选择 F。如果参与人 1 选择了 B（即芭蕾），则参与人 2 也应该选择 B。假设参与人 1 了解参与人 2 的这种选择行为并依此进行决策，那么参与人 1 应当选择 F。

评论：这个简单的例子告诉我们，在扩展式博弈里，参与人的行动计划和具体的选择是具有不同含义的两个概念。对于参与人 2 来说，当参与人 1 选择 F（B）时自己也选择 F（B）是行动计划，但是她最终选择的是 F（假设参与人 1 选择了 F）。我们称行动计划为策略（strategy），并称具体做出的选择为行动（action）。在单次博弈中二者并没有区别，因此我们统一采用策略一词。

我们会在 Chapter 4 和 Chapter 5 中学习扩展式博弈。上面给出的解所采用的分析方法叫逆向归纳法（backward induction），也称为子博弈完美纳什均衡（subgame perfect Nash equilibrium）。这并不是唯一一种纳什均衡。例如，假设参与人 1 选择 B，而参与人 2 的策略是无论参与人 1 如何选择，自己永远选择 B。此时，当给出对方的策略时，双方都没有更好的策略了，因此这个策略组合也是纳什均衡。但是，参与人 2 的策略并不是完全可信的，因为如果参与人 1 没有选择 B 而选择了 F，那么参与人 2 更应当选择 F 而不是 B。

1.3.3.2 序贯古诺博弈

故事：和前述的古诺博弈不同的是，这里假设公司 1 首先选择，而公司 2 可以观察公司 1 选择的结果。

模型：由于每个参与人 i=1,2 都有无穷多个备选项 q_i \geq 0，我们无法绘制类似 Figure 1.2 的决策树。这里我们用折线替代直线来表达连续空间上的行动集合，于是我们可以得到 Figure 1.3。参与人 1 首先选择 q_1 \geq 0，参与人 2 随后在确认 q_1 取值的情况下选择 q_2 \geq 0。

解：和序贯性别战博弈一样，这里我们也用逆向思维来分析。已知当参与人 2 知道 q_1 时，他对自身利润最大化的结果是 q_2 = \max\{\tfrac{1}{2}(1-q_1), 0\}。因此参与人 1 在决策中可以利用这个函数来最大化自己的利润函数，即

\max_{0 \leq q_1 \leq 1} q_1 \big[1 - q_1 - \tfrac{1}{2}(1-q_1)\big]

其解是 q_1 = \tfrac{1}{2}，对应 q_2 = \tfrac{1}{4}。

评论：这个解也是一个子博弈完美纳什均衡，在这个应用问题中也称作斯塔克伯格均衡（Stackelberg equilibrium），参照 Chapter 6。

1.3.3.3 市场进入与威慑（entry deterrence）

故事：在产业组织论中有一个古老的问题，说的是行业垄断企业能否通过威胁要开始价格战的方式阻止新企业进入该市场。我们可以考虑下面的情况来分析这个问题。假设有两个参与人，分别是新企业和垄断企业。新企业从进入（Enter）和不进入（stay Out）间进行选择。如果它选择了进入（E），则垄断企业可以选择和它共谋（Collude）或开始价格战（Fight）。该市场的利润在垄断价格下为 100，在价格战下为 0。新企业进入市场的成本是 10。当双方共谋时，它们将平分垄断价格下的利润。

模型：这个模型可以表达为 Figure 1.4。

解：根据逆向归纳法，新企业会选择进入市场，而垄断企业会选择共谋。

评论：和序贯性别战博弈类似，此博弈中也存在其他的纳什均衡，即新企业选择不进入市场，而垄断企业的策略是当新企业选择进入时自己选择开始价格战。读者应该很容易就能确认这两个策略是互为最佳响应的。在这个纳什均衡中我们依然可以说垄断企业的“威慑”策略是不可信的，因为它损害了自身的利益。

1.3.3.4 不完全信息下的市场进入与威慑（entry deterrence with incomplete information）

故事：现在我们考虑市场进入问题的另一种设定。假设垄断企业在选择开始价格战（F）时可以有 50\% 的概率获得正收益 x 而非 0（这里 x 是模型的参数而非变量）。新企业仍然首先进行选择，并且它知道垄断企业选择 F 时的收益是 x 还是 0。垄断企业随后进行选择，但是在选择时不知道该收益是 x 还是 0。双方都知道垄断企业获得 x 或 0 收益的概率。当新企业的体量是机密信息（private information）时这个设定就显得比较合理了。如果新企业的体量较小，无法应付价格战，则开始价格战后大部分市场还是会被垄断企业所占有，从而带来正利润。我们实际上是在假设垄断企业预测新企业体量较小的概率是 50\%，而新企业也了解这一点。

模型：以上设定可以通过在博弈树（game tree）中加入随机选择（chance move）节点来实现。这时的博弈树应当反映参与人之间的非对称信息结构。我们来看 Figure 1.5 中的博弈树。首先，其中有一个随机选择节点⁶。新企业在知道随机选择结果后选择是否进入市场。如果它选择进入，则垄断企业选择共谋或开始价格战，此时垄断企业不知道随机选择的结果，而这在图中表达为用虚线连接的两个节点。换句话说，垄断企业有两个决策节点，但是它不清楚自己究竟在二者中的哪个位置。因此它只能从 C 和 F 中进行选择，但无法将这些选项和随机选择的结果相结合。

解：如果 x \leq 50，则垄断企业选择 C 且新企业选择 E 依然是子博弈完美纳什均衡。另一个纳什均衡是无论随机选择的结果如何，新企业都选择 O 且垄断企业选择 F。如果考虑此博弈中的概率分布信息，则有一个新的解的概念称作完美贝叶斯均衡（perfect Bayesian equilibrium），我们将在 Chapter 5 中学习。

评论：用虚线连接起来的垄断企业的两个决策节点组成了一个信息集（information set）。一般情况下，信息集被用来给不完美信息（imperfect information）博弈建模。在这个例子中，由于垄断企业不知道随机选择的结果，导致产生不完美信息。另一种不完美信息源自一些参与人无法观察其他参与人的选择结果。例如在同时决策的性别战博弈中，参与人 2 在决策时不知道参与人 1 的选择是什么，如果我们用扩展式博弈进行建模，则可以得到 Figure 1.6 中的博弈树。

⁶ 通常解释为“外生”地决定哪种状态会真正实现，在这个例子中决定垄断企业选择 F 时的收益是 x 还是 0。

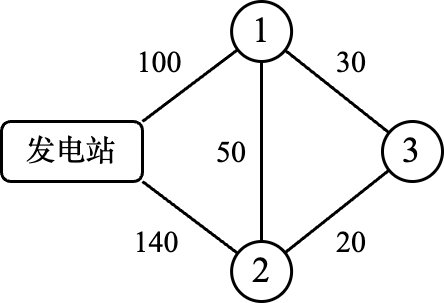
1.3.4 合作博弈

在合作博弈中，分析的焦点不再是策略的选择，而是关于收益和联盟（coalition）。常用的分析方法也不再是均衡分析，而变成了公理化方法。这背后隐藏着一个假设，即参与人之间可以形成具有约束力的约定。

1.3.4.1 三个城市间的合作

故事：城市 1、2、3 打算接入附近的一个发电站。输电网及其费用显示在 Figure 1.7 中。每个城市都可以租用任意一条输电线路。如果不同城市选择合作，则有可能减少整体租金（这里假设输电线路没有容量限制）。

模型：这个故事中的参与人是三个城市。令参与人集合为 N=\{1,2,3\}。参与人之间可以形成联盟（coalition）：N 的任意子集 S 都是一个联盟。每个可能的联盟的总输电成本及其能够节省下的金额汇总在 Table 1.1 中。

Table 1.1: 三个城市博弈

S	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
c(S)	100	140	130	150	130	150	150
v(S)	0	0	0	90	100	120	220

联盟 S 的总成本 c(S) 是连接发电成与联盟成员间最便宜路径的租金之和。能够节省下的金额 v(S) 是由联盟成员都各自租用输电线路时的租金之和减去联盟的总成本得到的，即

v(S) = \sum_{i \in S} c(\{i\}) - c(S)

(N,v) 定义了一个合作博弈（cooperative game）。

解：合作博弈 (N,v) 中的基本问题是哪个联盟能够真正成立，以及如何在联盟成员之间分配总收益（或总成本）。成立一个联盟需要所有成员同意，但是否同意加入联盟往往取决于在该联盟中可以获得多少利益。因此，第二个问题看上去更加的本质，因此这里我们主要关注分配问题。在合作博弈理论中，我们通常假设全体联盟（或大联盟，grand coalition）N 成立，然后讨论如何分配 v(N)。回到这个例子中就是怎样在三个城市间分配省下的 220 成本。更严密地说，我们是在寻找一个向量 \boldsymbol{x} = x_1 + x_2 + x_3 \in \mathbb{R}^3 使 x_1 + x_2 + x_3 = 220。这里 x_i, i \in \{1,2,3\} 代表参与人 i 的收益。首先浮现在脑海的候选可能是 x_1 = x_2 = x_3 = 220/3，但这无法反映例子中的非对称性，即某些联盟比其他联盟能够节省更多的成本。这一领域的文献中提供了很多不同的解，其中常用的包括核（core），Shapley 值（Shapley value）和 nucleolus。

核是一种无法通过子联盟获得更高收益的分配。在这个例子中，核分配满足下面的条件，

\begin{align*} & x_1 + x_2 + x_3 = 220, \\ & x_1 \geq 0, \ x_2 \geq 0, \ x_3 \geq 0, \\ & x_1 + x_2 \geq 90, \\ & x_1 + x_3 \geq 100, \\ & x_2 + x_3 \geq 120. \end{align*}

可见这是一个很大的集合，作为此问题的解并不合适。

而 Shapley 值是一个单值解（只包含一个分配向量）。粗略的说，Shapley 值分配给每个参与人的是他对各联盟做出贡献的平均值。我们可以想象让参与人们依此进入一间房间，例如按照 1-2-3 的顺序。当参与人 1 进入房间时，他自己就形成了一个单人联盟，其收益（节省的成本）为 0。当参与人 2 进入房间时，他与房间里的参与人 1 形成了新的联盟 \{1,2\}，此时参与人 2 的贡献为 v(\{1,2\}) - v(\{1\}) = 90 - 0 = 90。最后，参与人 3 走进房间并形成了全体联盟，而他的贡献为 v(N) - v(\{1,2\}) = 220-90 = 130。按照这个顺序进入房间会形成收益向量 (0,90,130)。Shapley 值是针对所有可能的顺序重复这一计算，并对结果取算数平均。这个例子对应的 Shapley 值是 (65, 75, 80)。

Nucleolus 也是一个单值解，在这个例子中为 (56\tfrac{2}{3}, 76\tfrac{2}{3}, 86\tfrac{2}{3})。Nucleolus 的定义更复杂，计算难度也更大，因此我们在这里暂时不做介绍。

以上概念的正式定义将在 Chapter 7 中介绍（或参照原书第九章）。

评论：此类博弈中有两个默认的假设：其一，能够成立的联盟都可以针对其收益分配形成具有约束力的约定；其二，不超过联盟可获得总价值的分配都是可行的。因此，这类博弈又被称作效用可转移合作博弈（cooperative games with transferable utility，或 TU-games）。

1.3.4.2 手套博弈（the glove game）

故事：考虑三个参与人 1、2、3。参与人 1 和 2 各自拥有一只右手的手套，而参与人 3 拥有一只左手的手套。一双手套的价值是 1。参与人们可以通过合作获得收益。

模型：这个例子的有关信息汇总在 Table 1.2 中。

Table 1.2: 手套博弈

S	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	0	0	0	1	1	1

解：此博弈的核只包含一个收益向量（你能找到吗？）。Shapley 值是 (1/6, 1/6, 2/3)。Nucleolus 与核一致。

1.3.4.3 排列博弈（a permutation game）

故事：小张、小李和小王分别在星期一、二、三约了牙医。但是这个安排对他们来说并不是最好的。Table 1.3 中用数字描述了三人对日期的偏好。

Table 1.3: 小张、小李和小王对看牙日期的偏好

	星期一	星期二	星期三
小张	2	4	8
小李	10	5	2
小王	10	6	4

模型：在这个故事中，联盟意味着成员之间可以自由地调换预约日期。例如，如果小张和小李成立联盟，则他们可以获得的总收益会从 7 上升为 14。此博弈可以总结为 Table 1.4。

Table 1.4: 牙医博弈：参与人 1、2、3 分别为小张、小李、小王

S	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	2	5	4	14	18	9	24

解：此博弈的核是由 (15,5,4), (14,6,4), (8,6,10), (9,5,10) 四点为顶点构成的四边形及其内部的点集。Shapley 值是 (9.5, 6.5, 8)。Nucleolus 是 (11.5, 5.5, 7)。

评论：排列博弈在原书第二十章中讨论。

1.3.4.4 投票博弈（a voting game）

联合国安全理事会中有五个常任理事国（分别是大不列颠及北爱尔兰联合王国、俄罗斯联邦、法国、美利坚合众国、中国⁷）和十个非常任理事国。若要通过一项动议需要包括所有常任理事国在内的至少九个理事国同意。这个例子对应一个有 15 个参与人的投票博弈 (N,v)，当联盟 S 包含五个常任理事国和至少另外四个非常任理事国时，有 v(S)=1，否则 v(S)=0。联盟总价值为 0 或 1 的合作博弈也称作基本博弈（或简单博弈，simple game）。价值为 1 的联盟也称为胜利联盟，反之价值为 0 的联盟称为失败联盟。基本博弈可在原书第十六章详细学习。

投票博弈的解可以解释为每个参与人对决议的影响力（voting power），而非收益或效用。

⁷ https://main.un.org/securitycouncil/zh/content/current-members

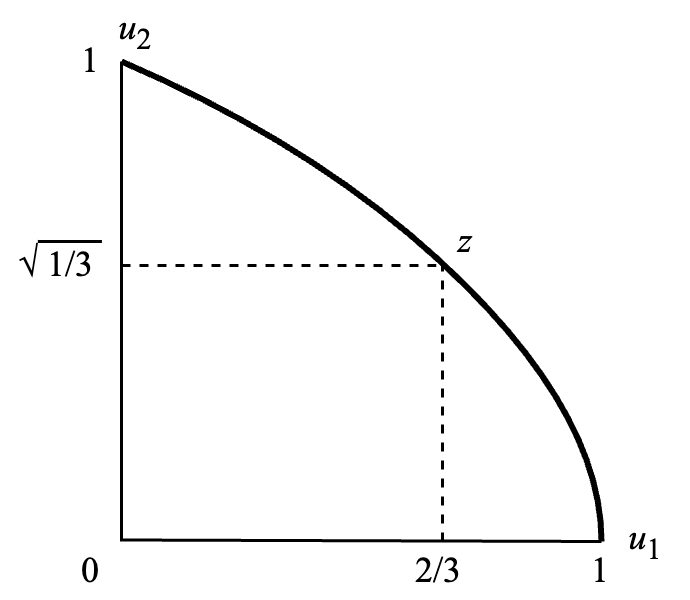
1.3.5 讨价还价博弈

讨价还价理论主要学习参与人间如何达成共识。

1.3.5.1 一个分配问题（a division problem）

故事：两个参与人需要针对如何分配一个单位的完美可分割物品（例如一升葡萄酒）达成共识。二人要么同意以 (\alpha, \beta), \alpha \geq 0, \beta \geq 0, \alpha + \beta \leq 1 的比例分配，要么什么也得不到。参与人对该物品的偏好以效用函数表达。

模型：为了方便分析，我们假设参与人 1 的效用函数是 u_1(\alpha) = \alpha，参与人 2 的效用函数是 u_2(\beta) = \sqrt{\beta}。此时，分配 (\alpha,1-\alpha) 对应的效用组合为 (\alpha, \sqrt{1-\alpha})。如果令 \alpha 在 0 和 1 之间变化，我们就能得到所有的效用组合，如 Figure 1.8 中的加粗曲线所示。两人所分得比例之和也可以小于 1，这对应着图中由曲线和两个坐标轴围起来的部分，我们称这部分及其边界为可行解。

解：根据纳什谈判解（Nash bargaining solution）的概念，此例子的解应该是可行解中使两个参与人的效用之积最大的点。由于该最大化问题的解必定在边界上，它等同于

\max_{0\leq \alpha \leq 1} \alpha \sqrt{1-\alpha}

最大值对应 \alpha = 2/3，因此此例子的最优分配为 (2/3, 1/3)，对应效用组合 (2/3, \sqrt{1/3})，即 Figure 1.8 中的点 z。那么采用纳什谈判解的理由是什么呢？因为它也可以用公理化的方式解释。

评论：在 Chapter 8 （或原书第十章）中有关于纳什谈判解的公理化讨论。在关于讨价还价的文献中也有很多基于非合作博弈的方法，例如鲁宾斯坦模型（Chapter 6）。这个讨价还价问题也可以看作效用不可转移合作博弈（cooperative game without transferable utility，或 NTU-game）的一个例子。TU-game 是 NTU-game 的子集。

1.4 合作博弈 vs 非合作博弈

合作博弈与非合作博弈的主要区别通常解释为合作博弈中存在有约束力的约定，而非合作博弈没有。这一区别其实并不是正式定义，而且也不十分清晰：例如，合作博弈中的核明显具有非合作的特性，而非合作博弈中的相关均衡（correlated equilibrium，见原书第十三章）明显具有合作的特性。在文献中也有不少研究用合作与非合作两个视角分析同一个问题，这有些时候被称为纳什计划（Nash program），前面的讨价还价问题就是它的一个例子。另外，博弈论中的实践（implementation）理论就是研究如何用某个非合作博弈的均衡来实现合作博弈的解。

相比之下，更加具有实际意义的区别在于建模方法：在非合作博弈中，参与人拥有具体的策略；而合作博弈则更加抽象，参与人和联盟是由他们可以获得的收益来刻画的。Section 1.3.1 ～ Section 1.3.3 中的例子都是非合作博弈，而 Section 1.3.4 和 Section 1.3.5 中的例子都是合作博弈。