7 合作博弈

本章内容基于原书第九章。

合作博弈的隐藏假设是参与人们可以结成联盟（coalition）并针对如何分配联盟带来的总收益达成具有约束力的协议。在合作博弈中，策略并不是模型的一部份，在这一点上它比非合作博弈更加抽象。合作博弈模型只描述了每个可能的联盟能够达成的收益。效用可转移合作博弈（TU-game）假设联盟的收益可以用一个数字表达。可以将其理解为货币价值，并且在联盟真正形成时可以通过任何可以想到的方式分配给联盟成员（也包括支付值为负的情况）。更具一般性的解释是可以在参与人之间相互转移的效用，例如假设效用可以通过某种交换媒介来衡量，而最常见的媒介就是货币。

这一章的内容是对效用可转移合作博弈理论的初步介绍。在 Sections 7.2-7.4 中我们将会讨论几个常见的解，包括核（core）、Shapley 值、以及 nucleolus¹。首先在 Section 7.1 中介绍例子和基本概念。

¹ 核（core）也可以翻译成“核心”。Shapley 通常翻译为夏普利，也有人写成沙普利。对 nucleolus 的常见翻译是沿用生物学中使用的“核仁”，注意英语发音时重音在 o 上。

7.1 例子和基本概念

在 Chapter 1 中我们介绍了几个效用可转移合作博弈的例子，包括三城博弈、手套博弈、排列博弈、以及投票博弈，这些博弈问题背后的故事可以参考 Section 1.3.4。这里我们只讨论博弈本身。

在三城博弈中，城市通过合作可以节省开支，具体的金额见 Table 7.1。此表中的第一行列出了所有可能出现的联盟。我们用“联盟”一词表达参与人集合的任意子集，因此联盟并不一定会真正结成。空集是任何集合的子集，因此空联盟也被加入到表中。这只是习惯问题，我们按照惯例为其赋值为零。表中第二行的数字是联盟的价值（worth）。例如，联盟 S = \{1,2\} 的价值是 90。在这个例子中，90 代表城市 1 和城市 2 通过合作能够节省的成本。如果这个联盟真正结成了，两个城市可以分配联盟的价值。具体的说就是当 x_1 \geq 0 和 x_2 \geq 0 满足 x_1 + x_2 \leq 90 时，参与人 1 可以获得 x_1，参与人 2 可以获得 x_2。

Table 7.1: 三城博弈

S	\emptyset	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	0	0	0	90	100	120	220

在手套博弈中，联盟的意义是组成一对手套。这个博弈的价值整理在 Table 7.2 中。例如全体联盟（grand coalition）\{1,2,3\} 的价值 1 代表其能够组成的一对手套的货币价值或效用值。在这里联盟成员也可以自由分配联盟的价值，因此全体联盟的分配可以是满足 x_1 + x_2 + x_3 \leq 1 的任意向量 (x_1, x_2, x_3) \in \mathbb{R}^3。在这里 x_i 既可以代表参与人 1 分到的金额，也可以解释成他戴手套的时间占比（仅限 x_i 为非负时）。

Table 7.2: 手套博弈

S	\emptyset	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	0	0	0	0	1	1	1

Table 7.3 重新描述了排列博弈（牙医博弈）。此博弈中联盟的价值可以解释为成员在牙医排期上节省的机会成本。而这当然也是可以在联盟成员间自由分配的。

Table 7.3: 排列博弈

S	\emptyset	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	2	5	4	14	18	9	24

至于联合国安理会的投票博弈，虽然也能用表格的形式记下所有联盟的价值，但是那将会是一个包含 2^{15} = 32768 个联盟的巨大表格。因此，对这个博弈来说更方便的表达方式是利用函数。令常任理事国为参与人 1, 2, 3, 4, 5，非常任理事国为参与人 6 - 15。令 N = \{1, \dots, 15\} 为全体联盟，v(S) 为联盟 S\subseteq N 的价值。则有

v(S) = \begin{cases} 1 & \text{if } \ \{1,\dots,5\} \subseteq S \text{ and } |S| \geq 9 \\ 0 & \text{otherwise} \end{cases}

其中 |S| 为联盟 S 的成员数。这里的数字 1 代表该联盟是胜利联盟（winning coalition），而数字 0 代表失败联盟（losing coalition）。在分析这类博弈时，最终分配中的 x_i 通常被解释为影响力指数（power index）。

下面的定义正式描述了例子中出现的基本概念。

Definition 7.1 效用可转移合作博弈（或 TU-game）表达为二元组 (N, v)，其中 N = \{1, \dots, n\}, n \in \mathbb{N} 是参与人集合，v 是赋予每个联盟 S \subseteq N 以实数值 v(S) 的函数，并假设 v(\emptyset) = 0。函数 v 称为特征函数（characteristic function），函数值 v(S) 称为联盟 S 的价值。联盟 N 称为全体联盟。给联盟 S 成员的收益分配（payoff distribution）或收益向量（payoff vector）是实数向量 (x_i)_{i \in S}。

在分析 TU-game 时，我们主要回答两个重要问题：哪个联盟会真正结成；如何在成员间分配联盟的价值。在本章中，我们只假设全体联盟会结成，然后集中精力讨论价值分配。这个设定并没有它的第一印象那么具有局限性，因为联盟能否结成自然地依赖于其利益分配方式。因此，即使更小的联盟可以结成，对于价值分配的讨论也是必要的。

7.2 核

考虑 Table 7.1 中的三城博弈。假设全体联盟成立，成员需要针对分配总价值 v(N) = 220 的方案 x_1=40, x_2=40, x_3=140 进行商议。或许我们可以猜测这个方案是参与人 3 提出的。针对此方案，参与人 1 和参与人 2 可以成功拒绝，因为在没有参与人 3 的情况下，他们两人可以共同获得 v(\{1,2\}) = 90 > 80 = x_1 + x_2 的价值。我们说这时 \boldsymbol{x} = (x_1,x_2,x_3) 不在博弈的核中。三城博弈的核是全体联盟 N=\{1,2,3\} 的收益分配中，各成员所得之和等于联盟价值 v(N) = 220，且任意非空联盟都获得不少于自身价值的收益分配的集合。该集合的数学表达式是

\begin{align*} C = \big\{ (x_1, x_2, x_3 \in \mathbb{R}^3 \ \mid \ & x_1, x_2, x_3 \geq 0 , \\ & x_1 + x_2 \geq 90, x_1 + x_3 \geq 100, x_2 + x_3 \geq 120 \\ & x_1 + x_2 + x_3 = 220) \big\} \end{align*}

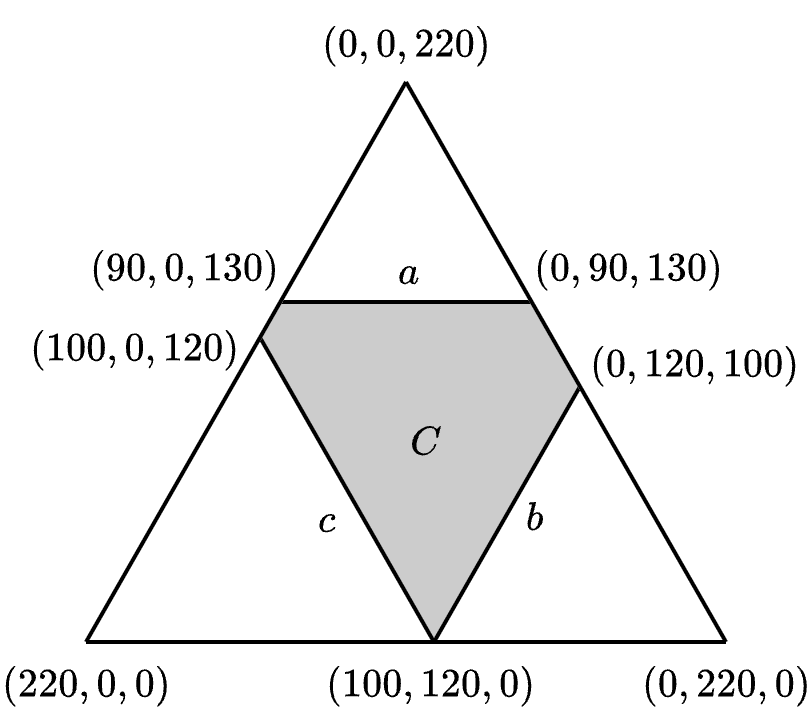
我们可以将它绘图以加深理解。虽然 C 是 \mathbb{R}^3 的子集，但约束条件 x_1 + x_2 + x_3 = 220 使它成为 \mathbb{R}^3 中一个二维平面的子集，即通过三点 (220,0,0), (0,220,0), (0,0,220) 的平面。Figure 7.1 绘制了以此三点为顶点的三角形。根据约束条件 x_1, x_2, x_3 \geq 0，集合 C 包含在这个三角形的内部。三个二人联盟的约束条件进一步将 C 限制在图中的阴影部份。

Figure 7.1: 集合 C（阴影部份）是三城博弈的核。线段 a 对应约束条件 x_1 + x_2 \geq 90，它包含三角形内部所有 x_1 + x_2 = 90 \Leftrightarrow x_3 = 130 的点；线段 b 对应约束条件 x_1 + x_3 \geq 100；线段 c 对应约束条件 x_2 + x_3 \geq 120。

因此，三城博弈的核是由 (100, 120, 0), (0, 120, 100), (0, 90, 130), (90, 0, 130) 和 (100, 0, 120) 为顶点组成的多边形的边和内部的所有点的集合。

下面我们给出核的正式定义。对于收益分配 \boldsymbol{x} = (x_1, \dots, x_n) \in \mathbb{R}^n 和非空联盟 S \subseteq N，令 x(S) := \sum_{i \in S} x_i 为联盟 S 的成员在收益分配 \boldsymbol{x} 中可以获得的总收益。

Definition 7.2 对于 TU-game (N,v)，收益分配 \boldsymbol{x} = (x_1, \dots, x_n) \in \mathbb{R}^n 可能有下列性质：

有效（efficient）：x(N) = v(N)，
个体理性（individually rational）：x_i \geq v(\{i\}), i \in N，
联盟理性（coalitionally rational）：x(S) \geq v(S), \emptyset \neq S \subseteq N。

(N,v) 的核是集合

C(N,v) = \big\{ \boldsymbol{x} \in \mathbb{R}^3 \mid x(N) = v(N) \text{ and } x(S) \geq v(S) \text{ for } \emptyset \neq S \subseteq N \big\}

也就是说，(N,v) 的核是所有有效的具有联盟理性的收益分配的集合。

博弈的核可能是很大的集合（如三城博弈），可能是很小的集合（如手套博弈的核仅包含一个收益分配 (0,0,1)），也可能是空集。一般情况下，核可以通过线性规划法计算。二人或三人博弈的核可以通过绘图法计算（例如上面的三城问题）。而有时，通过一些博弈的特殊性质也可以推导出该博弈的核。

在本节的最后，我们计算下面的广义手套博弈的核。

Example 7.1 (广义手套博弈) 假设有 \ell > 0 个参与人拥有一只左手的手套，其集合记为 L。有 r > 0 个参与人拥有一只右手的手套，其集合记为 R。参与人的总数为 n，即 n = \ell + r。全体联盟 N 包含所有参与人。联盟 S 的价值取决于其成员可以组成多少副手套。因此，v(S) 等于 S 中拥有左手手套的人数和拥有右手手套的人数的最小值，即

v(S) = \min \{ |S \cap L|, |S \cap R| \}.

即使我们给 \ell 和 r 赋予具体的值，我们也无法针对 \ell + r > 3 的情形应用前面介绍的绘图法计算此博弈的核（其实四人博弈是可以绘图的，但是得到的是复杂的三维图像）。因此我们需要用另一种方法进行分析。

首先，假设 \ell > r。此时 v(N) = r，因为全体联盟一共可以组成 r 副手套，这提供了核的一个约束条件 x_1 + \dots + x_n = r。每个参与人自己无法组成一幅手套，因此 v(\{i\}) = 0, i \in N，这提供了第二个约束条件 x_i \geq 0, i \in N。现在选择 L 中的一个参与人 j，即一个拥有左手手套的参与人。考虑包含所有拥有右手手套的参与人和 j 以外的 r 个拥有左手手套的参与人组成的联盟 S。我们知道 v(S) = r，因为 S 的成员可以组成 r 副手套，但是这也意味着他们获得的分配总额至少为 r，即 x(S) \geq r。由 x(N) = r 可得 x(S) = r，因此 x_j = 0。这个推导适用于任意一个拥有左手手套的参与人，因此他们的分配都为零。到此为止的结论是所有拥有右手手套的参与人获得的分配总额为 r，而每个拥有左手手套的参与人获得的分配为零。

现在假设 i 拥有一只右手手套，j 拥有一只左手手套。此时 v(\{i,j\}) = 1，因此 x_i + x_j \geq 1。我们已经知道 x_j = 0，因此 x_i \geq 1。此逻辑适用于任何拥有右手手套的参与人，且一共有 r 人，因此每个拥有右手手套的参与人获得的分配都是 1。至此，我们发现了唯一满足条件的收益分配：给每个拥有右手手套的参与人分配 1，给每个拥有左手手套的参与人分配 0。换句话说，如果 \boldsymbol{x} 在核中，那么它就是这个收益分配。

另一方面，这个收益分配确实在核中。所有参与人的分配额之和是 r，确实等于 v(N)。任意联盟 S 获得的分配额之和等于其中拥有右手手套参与人的人数，这也不小于 S 的价值。

总结以上分析可以得到在 \ell > r 时核的表达式

C(v) = \{\boldsymbol{x} \in \mathbb{R}^n \mid x_i = 1 \text{ for } i \in R, x_i = 0 \text{ for } i \in L \}.

同理，在 r > \ell 时核的表达式为

C(v) = \{\boldsymbol{x} \in \mathbb{R}^n \mid x_i = 1 \text{ for } i \in L, x_i = 0 \text{ for } i \in R \}.

你能自己计算 \ell = r 时的核吗？

7.3 Shapley 值

Shapley 值是一种完全不同于核的 TU-game 解。核是有可能为空的一个集合，但 Shapley 值会赋予每个 TU-game 的全体联盟一个唯一的收益分配。Shapley 值的定义并不是基于策略上的考量，而是给每个参与人分配其在博弈中的“平均边际贡献”（average marginal contribution）。在 Chapter 1 中我们已经给三城博弈定义了 Shapley 值，下面我们首先复习一下这个定义，并在此基础上进行扩展。

考虑 Table 7.1 中的三城博弈。我们可以想象让参与人们依次进入一间房间，每个参与人在进入该房间时会得到自己对房间中形成的联盟价值的贡献值。例如，令参与人 1 首先进入房间，然后依次是参与人 2 和 3。参与人 1 进入房间时房中没有其他人，因此他可以获得他的边际贡献 v(\{1\}) - v(\emptyset) = 0 - 0 = 0。当参与人 2 进入房间时，参与人 1 已经在房间中了，因此参与人 2 获得的边际贡献是 v(\{1,2\}) - v(\{1\}) = 90 - 0 = 90。到了参与人 3 进入房间时，房间中已经有联盟 \{1,2\}，因此参与人 3 可以获得他的边际贡献 v(\{1,2,3\}) - v(\{1,2\}) = 220 - 90 = 130。通过这个过程得出了一个收益分配 (0,90,130)，我们称之为边际向量（marginal vector）。当然了，这个分配并不能说是公正的，因为它依赖进入房间的顺序，并且这个顺序是我们随意决定的。事实上还有另外五种进入顺序可以考虑。Shapley 值是所有六种进入顺序对应的边际向量的平均值，见 Table 7.4。

Table 7.4: 三城博弈的 Shapley 值的计算过程

进入顺序	参与人 1	参与人 2	参与人 3
1, 2, 3	0	90	130
1, 3, 2	0	120	100
2, 1, 3	90	0	130
2, 3, 1	100	0	120
3, 1, 2	100	120	0
3, 2, 1	100	120	0
总和	390	450	480
Shapley 值	65	75	80

对于任意 TU-game (N,v)，Shapley 值都可以用相同的方式计算。参与人集合为 N = \{1,\dots,n\} 时，共有 n\cdot (n-1) \cdot \dots \cdot 2\cdot 1 = n! 种排列方式。首先计算每种排列方式对应的边际向量，然后在计算它们的均值即可。但是如果参与人的数量太多，就过导致计算量过大。以联合国安理会的投票博弈为例，我们需要计算 15! > 13 \times 10^{11} 个边际向量，这显然是不现实的。当然，我们还有其他更加聪明的方法计算参与人的总边际贡献。

我们以一个十人 TU-game 为例进行说明。考虑参与人 7 和联盟 \{3, 5, 9\}。这时的边际贡献 v(\{3,5,7,9\} - v(\{3,5,9\}) 可以由多个不同的边际向量产生。那么具体有多少个呢？首先，参与人 3、5、9 需要率先进入房间，这对应 3! 种不同的进入顺序。此后参与人 7 进入房间。最后，剩下的六个参与人进入房间，而这对应 6! 种不同的进入顺序。因此，能让参与人 7 获得边际贡献 v(\{3,5,7,9\} - v(\{3,5,9\}) 的边际向量一共有 3! \times 6! 种。这种计算方法可以大幅降低计算量。

现在我们将这种方法应用在任意的 TU-game (N,v) 的任意参与人 i 和任意不包含 i 的联盟 S 上。能让参与人 i 获得边际贡献 v(S \cup \{i\}) - v(S) 的边际向量的总数等于 S 中参与人的排列数 |S|! 与在参与人 i 之后进入房间的参与人的排列数 (n - |S| - 1)! 的乘积。因此，参与人 i 在联盟 S 成员之后进入房间时获得的总边际贡献为

|S|! (n - |S| - 1)! \big[ v(S \cup \{i\}) - v(S) \big].

参与人 i 的 Shapley 值就是通过对所有不包含 i 的联盟 S 对应的总边际贡献进行加总，然后除以联盟总排列数 n! 获得。实际上，我们也习惯用这种方式定义 Shapley 值。

Definition 7.3 TU-game (N,v) 的 Shapley 值记作 \Phi(N,v)。它的第 i 个要素，也就是参与人 i 的 Shapley 值是

\Phi_i(N,v) = \sum_{S\subseteq N: i\notin S} \frac{|S|! (n - |S| - 1)!}{n!}\big[ v(S \cup \{i\}) - v(S) \big].

在文献中你可能看到 Shapley 值的另一种表达方式

\Phi_i(N,v) = \sum_{S\subseteq N: i\in S} \frac{(|S|-1)! (n - |S|)!}{n!}\big[ v(S) - v(S \setminus \{i\}) \big]

在人数较多的 TU-game 中，用 Definition 7.3 中的公式计算 Shapley 值会更简单。但在证明一些性质的时候，基于边际向量的定义可能更好用。

三城博弈的 Shapley 值包含在核中（你需要确认一下）。但这并不是可推广的结论，在有些具有非空核的博弈中，Shapley 值也可能落在核的外侧。

Example 7.2 (广义手套博弈-续) 我们继续考虑 Example 7.1 中的广义手套博弈。这里假设 \ell = 4, r = 2。此时全体联盟的价值为 v(N) = 2。首先根据对称性，所有拥有左手手套的参与人都有相同的 Shapley 值，拥有右手手套者亦然（你可以尝试证明这个性质）。如果设每个拥有左手手套的参与人的 Shapley 值都是 \alpha，则每个拥有右手手套的参与人的 Shapley 值应为 (2-4\alpha)/2。下面我们来计算 \alpha。

假设 i 拥有一只左手手套。则 i 对成员中拥有左手手套者少于拥有右手手套者的任意联盟的边际贡献都是 1，对任意其他联盟的边际贡献都是 0，因此我们只需考虑前者。选取一个成员中拥有右手手套者人数为 k，拥有左手手套者人数为 j ，满足 j < k 且不包含 i 的联盟 S。此时 v(S) = j，v(S \cup \{i\}) = j+1，因此 v(S \cup \{i\}) - v(S) = 1。这样的联盟 S 共有 \binom{2}{k} \cdot \binom{3}{j} 个²。因为 |S| = k + j，Definition 7.3 中的权重等于 (k+j)!(5-k-j)!。因此，i 的 Shapley 值是

\Phi_i(N,v) = \alpha = \sum_{k=1}^2 \sum_{j = 0}^{k-1} \frac{(k+j)!(5-k-j)!}{6!} \binom{2}{k} \cdot \binom{3}{j}

经过简单计算可得 \alpha = 2/15。因此，

\Phi_i(N,v) = \begin{cases} 2/15 & \text{（如果 $i$ 拥有左手手套）}\\ 11/15 & \text{（如果 $i$ 拥有右手手套）} \end{cases}

注意此博弈的 Shapley 值不包含在核中。

以上分析方法可以用于任意的 \ell 和 r。如果 \ell = r，则根据对称性，每个参与人的 Shapley 值都是 1/2。

² \binom{p}{q} = \frac{p!}{q! (p-q)!} 是从 p 个对象中挑选 q 个对象的组合数。

Shapley 值的定义中给每个参与人赋予他平均边际贡献的含义本身可以看作是对这个解的正当性提供的支持。在文献中，有更多关于 Shapley 值的公理化分析。公理化的过程如下。考虑任意一个能给每个定义在 N 上的博弈赋予一个收益向量的函数（Shapley 值就是一个函数）。然后为函数定义一些性质或公理（axiom）。这些公理的作用是限制函数的可能性。如果公理越强，则满足公理的函数越少。如果公理足够强，就能将满足它们的函数减少为一个。这时就可以理解成用这些公理“定义”了一个函数。公理化方法是合作博弈研究领域的标准方法。

7.4 Nucleolus

本章中介绍的最后一个概念是 nucleolus。它和 Shapley 值一样都是单值解，即赋予每个 TU-game 一个收益分配。它比 Shapley 值更具吸引力的地方是当博弈的核为非空时，nucleolus 永远会得到一个核内部的收益分配³。Nucleolus 仅能定义在具有下列性质的博弈中。当一个 TU-game (N,v) 满足 v(N) \geq \sum_{i\in N} v(\{i\}) 时，我们说这个博弈是必要的（essential）。必要博弈存在有效且具有个人理性的全体联盟收益分配，我们将这样的收益分配称为 imputation⁴。TU-game (N,v) 的 imputation 集定义为

³ 或许这就是这个名字的来源，在生物学中，细胞的核仁（nucleolus）是细胞核（nucleus）内部的一种结构。

⁴ Impute 一词的常见含义是归咎、归责、归因或归属。在统计学中，imputation 是通过推测对缺失数据进行填补的方法。在经济和金融领域，imputation 可以指通过最终价格推测要素价格（theory of imputation），也可以指在计税时将纳税人的非现金所得换算为收入的方法（imputed income，推算收入）。这里我们不对博弈论中的 imputation 进行翻译。

I(N,v) = \big\{ \boldsymbol{x}\in \mathbb{R}^n \mid x(N) = v(N), x_i \geq v(\{i\}) \text{ for all } i \in N \big\}.

因此，当且仅当 I(N,v) \neq \emptyset 时，博弈 (N,v) 是必要博弈。

I(N,v) \neq \emptyset 时，(N,v) 为必要博弈是显而易见的。反之，你需要找出任意必要博弈 (N,v) 中的至少一个 imputation。

现在假设 (N,v) 是必要的 TU-game，令 \boldsymbol{x} \in I(N,v)，令 S \neq N 为一个非空联盟。定义 e(S, \boldsymbol{x}) 为联盟 S 在分配 \boldsymbol{x} 的超额值（excess），即 S 能够产生的价值与 \boldsymbol{x} 赋予 S 成员的总收益之差。具体表达为

e(S,\boldsymbol{x}) = v(S) - x(S).

超额值可以看作是联盟 S 对 imputation \boldsymbol{x} 的不满意度，因为当 \boldsymbol{x} 分配给 S 的总收益越小时，e(S, \boldsymbol{x}) 越大。如果超额值为正，则说明 S 获得的总收益小于它产生的价值。

如果用语言描述的话，一个必要的 TU-game 的 nucleolus 的定义如下。

首先，每一个收益分配 \boldsymbol{x} 都能对除了 N 和 \emptyset 以外的所有联盟计算超额值。找出令最大超额值最小的 imputation 的集合。如果该集合为单点集，则该点即为 nucleolus。
如果上面找出的 imputation 集不是单点集，则针对 (1) 中产生最大超额值的联盟以外的其他联盟，在 (1) 中确定的 imputation 集里找出令这些最大超额值最小的子集。如果这个子集是单点集，则该点为 nucleolus。
如果上一步没有确定 nucleolus，则重复 (2) 中的方法继续缩小 imputation 集。如果这次获得了一个单点集，则该点为 nucleolus。
如果还没有确定 nucleolus，则重复上面的过程，直至剩下的集合变成单点集为止。

因此，nucleolus 的出发点是让最大的不满意度尽可能的小。如果有两种以上不同的方法能够达到这一目的，则继续让第二大的不满意度尽可能的小。依此类推，直至获得唯一的收益分配。

原书第十九章给出了 nucleolus 的正式定义。这里我们仅通过例子展示 nucleolus 的计算过程。

Table 7.5: 三城博弈的 nucleolus 的计算过程示意

S	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	0	0	90	100	120	220
e(S, (70,70,80))	-70	-70	-80	-50	-50	-30
e(S, (56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3}))	-56\frac{2}{3}	-76\frac{2}{3}	-86\frac{2}{3}	-43\frac{1}{3}	-43\frac{1}{3}	-43\frac{1}{3}

第一个例子是三城博弈，见 Table 7.5。表格的第三行给出了每个联盟在 (70,70,80) 的超额值。选取这个 imputation 没有特殊的考量，仅仅是作为一个计算 nucleolus 的起点。在这个 imputation 上，最大的超额值为联盟 \{2,3\} 的 -30。这个值可以通过削减参与人 1 的分配并补贴给参与人 2 和 3 来降低，这同时也会令联盟 \{1,2\} 或 \{1,3\} 或两者的超额值上升。这两个联盟在 (70,70,80) 的超额值都是 -50。通过给参与人 2 和 3 各自增加 6\frac{2}{3} 的收益，同时降低参与人 1 的收益 2\cdot 6\frac{2}{3} = 13\frac{1}{3} 可以获得收益分配 (56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3})，使三个二人联盟的超额值都等于 -43\frac{1}{3}，也是新的最大超额值。注意，此时的最大超额值已经不能再小了，这是因为三个二人联盟在任意 imputation 的超额值之和都应该等于 -130，即

\begin{align*} e(\{1,2\}, \boldsymbol{x}) + e(\{1,3\}, \boldsymbol{x}) + e(\{2,2\}, \boldsymbol{x}) &= v(\{1,2\}) + v(\{1,3\}) + v(\{2,3\}) \\ & \phantom{= \ } - 2 (x_1 + x_2 + x_3) \\ &= 90 + 100 + 120 - 2 \cdot 220 \\ &= -130 . \end{align*}

这意味着若想继续降低某个二人联盟的超额值，势必要增加另一个二人联盟的超额值，使得最大超额值也随之增加。另外，能够使三个二人联盟的超额值达到一致的 imputation 只有一个，因为下面的方程组

\begin{align*} 90 - x_1 - x_2 &= 100 - x_1 - x_3 \\ 90 - x_1 - x_2 &= 120 - x_2 - x_3 \\ x_1 + x_2 + x_3 &= 220 \\ x_1, x_2, x_3 &\geq 0 \end{align*}

只有一个解，即 (56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3})。因此，这个收益分配就是三城博弈的 nucleolus。

这个例子好像在说，至少对三人 TU-game，nucleolus 可以简单地通过让三个二人联盟的超额值相等来计算。事实上这是不正确的。只有当二人联盟的价值远大于单人联盟的价值时，用这个方法才能够得到 nucleolus，否则就可能失败。让我们考虑 Table 7.6 中的三城博弈的变体，即将 v(\{1\}) 改为 20。在这个博弈中，(56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3}) 依然是 imputation，各联盟在它的超额值记载在表格的第三行。现在，最大超额值变成了参与人 1 的单人联盟的 -36\frac{2}{3}。(56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3}) 不再是 nucleolus 了，因为通过增加参与人 1 的分配同时减少参与人 2 或 3 的分配可以降低 \{1\} 的超额值。例如令 \{1\} 和 \{2,3\} 的超额值相等，即方程 20 - x_1 = 120 - x_2 - x_3。这和方程 x_1 + x_2 + x_3 = 220 一起可得 x_1 = 60, x_2 + x_3 = 160。如果将参与人 1 的分配从 56\frac{2}{3} 增至 60，同时减少参与人 2 和 3 的分配各 1\frac{2}{3}，可得收益分配 (60, 75, 85)。在这个新的 imputation 上的超额值记载在 Table 7.6 的第四行。现在我们来确认它就是这个博弈的 nucleolus。最大超额值是产生于联盟 \{1\} 和 \{2,3\} 的 -40，且不可继续降低，因为降低其中一个联盟的超额值必将同时增加另一个联盟的超额值。因此，在 nucleolus 中 x_1 的收益等于 60。第二大的超额值是产生于联盟 \{1,2\} 和 \{1,3\} 的 -45。因为 x_1 的收益已经固定了，现在降低这两个联盟其中一个的超额值意味着另一个联盟的超额值会随之增加。因此，x_2 和 x_3 的收益分别为 75 和 85。

Table 7.6: 三城博弈变体（v(\{1\}) = 20）的 nucleolus 的计算过程示意

S	\{1\}	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	20	0	0	90	100	120	220
e(S, (56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3}))	-36\frac{2}{3}	-76\frac{2}{3}	-86\frac{2}{3}	-43\frac{1}{3}	-43\frac{1}{3}	-43\frac{1}{3}
e(S, (60, 75, 80))	-40	-75	-85	-45	-45	-40

通过以上两个例子可以看出，计算 nucleolus 并不总是一件简单的事。对于三人博弈，上面展示的方法通常情况下是好用的。而更加通用的解法是解一系列由博弈导出的线性规划问题。下面我们以三城博弈为例进行讲解。

Example 7.3 针对 Table 7.5 中的三城博弈，其 nucleolus 中的最大超越值可以通过下面的线性最小化问题解出。

\begin{align*} \mathrm{minimize}\ \ \alpha \ \text{ subject to } \quad \quad x_1 + x_2 + x_3 &= 220 \\ x_1, x_2, x_3 &\geq 0 \\ 0 - x_1 & \leq \alpha \\ 0 - x_2 & \leq \alpha \\ 0 - x_3 & \leq \alpha \\ 90 - x_1 - x_2 & \leq \alpha \\ 100 - x_1 - x_3 & \leq \alpha \\ 120 - x_2 - x_3 & \leq \alpha \end{align*}

因此，\alpha 是最小化后的最大超越值。前两个约束条件确保 \alpha 的取值范围满足收益分配是 imputation。第三至第五个约束条件对单人联盟的超越值进行了限制，最后三个约束条件则对二人联盟的超越值进行了限制，即它们的超越值不会大于 \alpha。在这个问题中，利用 x_1 + x_2 + x_3 = 220 可以将变量数由四个减少为三个，例如 \alpha, x_1, x_2，然后通过绘图法找到最优解。而一般情况下，我们可以利用数值计算软件提供的诸如 simplex 法等通用方法进行求解。从前文的分析中我们已经知道最优解是 \alpha = -43\frac{1}{3}，对应的收入分配是 (x_1, x_2, x_3) = (56\frac{2}{3}, 76\frac{2}{3}, 86\frac{2}{3})。

而针对 Table 7.6 中的三城博弈变体，最小化问题则变为

\begin{align*} \mathrm{minimize}\ \ \alpha \ \text{ subject to } \quad \quad x_1 + x_2 + x_3 &= 220 \\ x_1, x_2, x_3 &\geq 0 \\ 20 - x_1 & \leq \alpha \\ 0 - x_2 & \leq \alpha \\ 0 - x_3 & \leq \alpha \\ 90 - x_1 - x_2 & \leq \alpha \\ 100 - x_1 - x_3 & \leq \alpha \\ 120 - x_2 - x_3 & \leq \alpha \end{align*}

从前文分析中可知此问题的解是 \alpha = -40，且所有能够达成此 \alpha 的收益分配都满足 x_1 = 60 和 x_2 + x_3 = 160。由此可以获得最小化第二大超越值所需的线性规划问题

\begin{align*} \mathrm{minimize}\ \ \alpha \ \text{ subject to } \quad \quad x_2 + x_3 &= 160 \\ x_2, x_3 &\geq 0 \\ - x_2 & \leq \alpha \\ - x_3 & \leq \alpha \\ 30 - x_2 & \leq \alpha \\ 40 - x_3 & \leq \alpha \end{align*}

最优解为 \alpha = -45，对应的收益分配为 (x_2, x_3) = (75, 85)。你可以尝试用绘图法进行确认。至此可知这个博弈的 nucleolus 是 (60, 75, 85)。

虽然 nucleolus 计算起来比较复杂，但是它能给每个必要博弈赋予一个 imputation 集合中的收益分配作为唯一解，而且当该博弈的核为非空时，nucleolus 永远在核的内部。这是 nucleolus 最吸引人的性质。

Proposition 7.1 令 (N,v) 为具有非空核的 TU-game。此时 (N,v) 的 nucleolus 在核的内部。

Proof. 考虑 (N,v) 的核内部的任意收益分配 \boldsymbol{x}。对每一个非空联盟 S \neq N 都有 x(S) \geq v(S)，因此 e(S,\boldsymbol{x}) = v(S) - x(S) \leq 0。假设 \boldsymbol{z} 是 (N,v) 的 nucleolus。已知 nucleolus 在 imputation 集合的范围内最小化最大超越值，\boldsymbol{x} 是一个 imputation 并且其所有超越值都为非正，因此可知 \boldsymbol{z} 中的最大超越值应为非正，因此 \boldsymbol{z} 的所有超越值都为非正。也就是说，对每一个非空联盟 S \neq N 都有 e(S, \boldsymbol{z}) = v(S) - z(S) \leq 0，因此 z(S) \geq v(S)。最后一个不等式意味着 \boldsymbol{z} 在 (N,v) 的核的内部。

根据 Proposition 7.1，如果已知一个博弈的核，则可以利用这一信息帮助我们计算 nucleolus。这里通过下面两个例子进行展示。

Example 7.4 考虑 Table 7.7 中的三人博弈。这个博弈的核为非空，且核中的任意收益分配都会赋予参与人 1 以零收益（你能确认这个结论吗）。我们以核中的一个分配 (0,10,10)开始计算。此分配的最大超越值为 0，由联盟 \{1\}，\{1,2\} 和 \{2,3\} 产生。这个最大超越值明显无法继续降低，因为降低 \{1\} 的超越值会增加 \{2,3\} 的超越值，反之亦然。因此，如果 \boldsymbol{z} 是 nucleolus，则 z_1 = 0，z_2 + z_3 = 20。接下来我们看另一个收益分配 (0,15,5)。这个分配的最大超越值也是 0，第二大超越值是 -5，由联盟 \{1,2\}，\{1,3\} 和 \{3\} 产生。因为 z_1 = 0 已经被固定了，如果要降低 \{1,2\} 的超越值则必须要增加 \{1,3\} 和 \{3\} 的超越值。因此可得 0 - z_3 = -5，即 z_3 = 5。因此，此博弈的 nucleolus 为 (0,15,5)。

Table 7.7: Example 7.4 中的博弈

S	\{2\}	\{3\}	\{1,2\}	\{1,3\}	\{2,3\}	\{1,2,3\}
v(S)	0	0	10	0	20	20
e(S, (0,10,10))	-10	-10	0	-10	0
e(S, (0, 15, 5))	-15	-5	-5	-5	0

Example 7.5 考虑 Section 7.2 中的广义手套博弈。当 \ell > r 时，核中仅包含一个收益分配，即拥有右手手套的参与人的收益为 1，拥有左手手套的参与人的收益为 0。根据 Proposition 7.1，这也是该博弈的 nucleolus。

作为本章的总结，我们计算下面例子中博弈的核、Shapley 值和 nucleolus。

Example 7.6 这里我们定义一个六人合作博弈。参与人集合为 N = \{1,\dots, 6\}。联盟 S 仅在下列情形之一时产生价值 1：要么 S 由参与人 1 和至少另一个参与人组成，要么 S = \{2,\dots,6\}。所有其他联盟的价值都为 0。（此博弈被称为 apex game，参与人 1 是 apex player，其他参与人是 minor player）

首先我们来确认此博弈的核为空集。假设 \boldsymbol{x} 是一个核分配，则有 x_1 + \dots + x_5 \geq v(\{1,\dots, 5\}) = 1。由于 x_6 \geq v(\{6\}) = 0，且 x_1 + \dots + x_6 = v(N) = 1，可得 x_1 + \dots + x_5 = 1，x_6 = 0。同理也可以推出 x_2 = \dots = x_5 = 0。因此 x_2 + \dots + x_6 = 0。但是这意味着 1 = v(\{2,\dots,6\}) > x_2 + \dots + x_6，不满足核的条件。由此可知核为空集。

对于 nucleolus，根据博弈的对称结构，我们可以假设它表达为 (1-5\alpha,\alpha, \dots, \alpha)。为了使其成为 imputation，我们还需要求 0 \leq \alpha \leq 1/5。对于每个 i \in \{2,\dots,6\}，联盟 \{1,i\} 的超越值都是 1 - (1-5\alpha) - \alpha = 4\alpha。联盟 \{2,\dots,6\} 的超越值为 1-5\alpha。显然只有这两个超越值可能成为最大超越值（你需要检验这一点）。如果我们增加 \alpha，则联盟 \{1,i\} 的超越值会增加，\{2,\dots,6\} 的超越值则会降低；而降低 \alpha 会带来相反的效果。因此，令最大超越值最小的条件是 4\alpha = 1-5\alpha，可得 \alpha = 1/9。因此 nucleolus 为 (4/9, 1/9, \dots, 1/9)。

Shapley 值可以通过 Definition 7.3 的表达式计算。首先计算参与人 2 的 Shapley 值。注意参与人 2 仅在加入联盟 \{1\} 和联盟 \{3,\dots,6\} 时会产生边际贡献 1，其他情况下的边际贡献都是 0，因此，

\Phi_2(N,v) = \frac{1!(6-1-1)!}{6!} \cdot 1 + \frac{4!(6-4-1)!}{6!} \cdot 1 = \frac{1}{15} 从博弈的对称结构可知其 Shapley 值为

\Phi(N,v) = \Big(1-5\cdot \frac{1}{15}, \frac{1}{15}, \dots, \frac{1}{15} \Big) = \Big( \frac{2}{3}, \frac{1}{15}, \dots, \frac{1}{15} \Big).