3 二人博弈
在这一章里我们讨论具有有限策略的二人博弈。与 Chapter 2 不同的是,我们不再要求参与人的收益之和为零(或为某个固定常数)。这使这一类博弈可以包含众多经济学中的应用问题,例如 Section 1.3.2 中的囚徒困境和性别战。
我们将在 Section 3.1 中介绍纳什均衡的概念。在 Section 3.2 中我们将展示如何计算任意博弈中的纯策略纳什均衡,如何在每个参与人只有两个策略的博弈中找到所有的纳什均衡,如何利用严格优势简化纳什均衡的计算,以及如何在规模更大的博弈中计算均衡。原书第十三章提供了更加深入和全面的讲解。
3.1 基本定义
有限策略二人博弈的数据可以用两个矩阵表达。但是通常我们将这两个矩阵简化为一个要素为二维向量的矩阵。因此此类博弈也称为双矩阵博弈(bimatrix game)。
在双矩阵博弈 (A,B) 中,如果参与人 1 选择行 i,参与人 2 选择列 j,则参与人 1 的收益为 a_{ij},参与人 2 的收益为 b_{ij}。与 Chapter 2 相同,参与人 1 的(混合)策略是关于行的概率分布 \boldsymbol{p},即下面集合的一个要素
\Delta^m := \big\{\boldsymbol{p} = (p_1, \dots, p_m) \in \mathbb{R}^m \mid \sum_{i=1}^m p_i = 1, p_i \geq 0 \text{ for all } i = 1, \dots, m \big\}
同样,参与人 2 的(混合)策略是关于列的概率分布 \boldsymbol{q},即下面集合的一个要素
\Delta^n := \big\{\boldsymbol{q} = (q_1, \dots, q_n) \in \mathbb{R}^n \mid \sum_{j=1}^n q_j = 1, q_j \geq 0 \text{ for all } j = 1, \dots, n \big\}
参与人 1 的策略 \boldsymbol{p} 如果满足某一行 i 对应的 p_i = 1,则称该策略为纯策略,也可以写作 \boldsymbol{e}^i。同样,参与人 2 的纯策略满足某一列 j 对应的 q_j = 1,也可以写作 \boldsymbol{e}^j。如果参与人 1 选择策略 \boldsymbol{p} 而参与人 2 选择策略 \boldsymbol{q},则二人的收益分别为
\boldsymbol{p} A \boldsymbol{q} = \sum_{i=1}^m \sum_{j=1}^n p_i a_{ij} q_j , \quad \boldsymbol{p} B \boldsymbol{q} = \sum_{i=1}^m \sum_{j=1}^n p_i b_{ij} q_j
矩阵 A 和 B 通常被简化为一个双矩阵,即将二者的 (i,j) 要素以向量 (a_{ij}, b_{ij}) 的形式放在一个矩阵的 (i,j) 位置,参照 Section 1.3.2 中的例子。
Section 1.3.2 中囚徒困境博弈的双矩阵表达
\begin{align*} & \begin{matrix} \ \ \ \ \ C & \ \ \ \ \ \ \ \ \ \ D \end{matrix} \\ \begin{matrix} C \\ D \end{matrix} \ \Bigg( & \begin{matrix} \, -1, -1 & -10, 0 \, \\ \, 0, -10 & -9, -9 \, \end{matrix} \Bigg) \end{align*}
1 或者说以自身利益为首要目标。
非合作博弈的核心概念是最佳响应(best reply)。它主张一个理性且自私1的参与人在知道(或预测)对方的策略的基础上,永远以最大化自己的(期望)收益为准则选择策略。
在纳什均衡中,每个参与人的策略都是对方策略的最佳响应。
纳什均衡的概念可以应用在任意的博弈上,即对参与人数、策略集合和收益函数不做任何限制。在后面的章节中我们将看到更多例子。
每个双矩阵博弈都存在纳什均衡(证明见原书第十三章)。一般来说,纳什均衡的主要问题并不是它的存在性,而是它往往并非唯一,以及如何理解它的含义。在很多博弈中存在多个纳什均衡,此时我们面临的问题是如何从中进行选择,即均衡的精炼(refinement)。而关于如何理解,一个古老的问题是参与人在现实中是否会(以及如何)选择均衡策略,纳什均衡的定义中并没有给出答案。
针对 Definition 3.3 中的混合策略纳什均衡,常常有人质疑混合策略究竟意味着什么。是像字面意思所说的,参与人从纯策略中随机选择一个吗?一个更加被认可的解释是策略选的不确定性,例如参与人 2 在考虑参与人 1 可能选择的策略时并不是完全确定的,因此他会认为参与人 1 的策略服从某个关于纯策略集合的概率分布,这个概率分布就是参与人 1 的混合策略。
现阶段我们暂时把关于如何解释混合策略的讨论放在一边,而单纯的依照字面意思理解纳什均衡。接下去我们将展示计算纯策略纳什均衡的通用方法,以及如何在每个参与人都只拥有两个策略的博弈中找到全部纳什均衡。我们也将讨论严格劣势策略的作用。
3.2 如何计算纳什均衡
针对任意双矩阵博弈找出所有纳什均衡并不是一件简单的事情。这里我们首先考虑一个更简单的问题,即针对任意双矩阵博弈找出所有纯策略纳什均衡,然后展示如何用图形分析发找出任意 2\times 2 博弈的所有纳什均衡。同样的方法也可以用在 2\times 3 或 3 \times 2 博弈上,但是我们不展开讨论。对于更大的博弈,图形分析法就不适用了(因为无法将四维空间可视化)。
3.2.1 纯策略纳什均衡
为了在双矩阵博弈中找到纯策略纳什均衡,我们可以首先针对参与人 1 的每个纯策略找出参与人 2 的最佳响应纯策略,然后针对参与人 2 的每个纯策略找出参与人 1 的最佳响应纯策略,最后从以上纯策略的组合中找出互为最佳响应的那些即可。例如考虑下面的博弈
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ X & \ \ \,Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ M \\ B \end{matrix} & \begin{pmatrix} 2,2 & 4,0 & 1,1 & 3,2 \\ 0,3 & 1,5 & 4,4 & 3,4\\ 2,0 & 2,1 & 5,1 & 1,0 \end{pmatrix} \end{align*}
首先我们尝试找出参与人 1 的每个纯策略对应的参与人 2 的最佳响应纯策略,这可以用下划线的形式在矩阵中标出:
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ X & \ \ \,Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ M \\ B \end{matrix} & \begin{pmatrix} 2,\underline{2} & 4,0 & 1,1 & 3,\underline{2} \\ 0,3 & 1,\underline{5} & 4,4 & 3,4\\ 2,0 & 2,\underline{1} & 5,\underline{1} & 1,0 \end{pmatrix} \end{align*}
下一步是找出参与人 2 的每个纯策略对应的参与人 1 的最佳响应纯策略,在前一个矩阵的基础上继续以下划线的形式标出:
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ X & \ \ \,Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ M \\ B \end{matrix} & \begin{pmatrix} \underline{2},\underline{2} & \underline{4},0 & 1,1 & \underline{3},\underline{2} \\ 0,3 & 1,\underline{5} & 4,4 & \underline{3},4\\ \underline{2},0 & 2,\underline{1} & \underline{5},\underline{1} & 1,0 \end{pmatrix} \end{align*}
由此可知,此博弈有三个纯策略纳什均衡:(T, W), (T, Z) 和 (B, Y)。如果用混合策略的方式表达,这三个纳什均衡分别为 (\boldsymbol{e}^1, \boldsymbol{e}^1), (\boldsymbol{e}^1, \boldsymbol{e}^4) 和 (\boldsymbol{e}^3, \boldsymbol{e}^3),或者 ((1,0,0), (1,0,0,0)), ((1,0,0), (0,0,0,1)) 和 ((0,0,1), (0,0,1,0))。
严格的讲,我们在寻找一个纯策略的最佳响应时还应该考虑混合策略,以便判断最佳响应纯策略是否真的是“最佳”。然而,并不难发现最佳响应混合策略都是最佳响应纯策略的凸组合,因此无法带来比最佳响应纯策略更高的收益。例如在上面的例子中,针对参与人 1 的策略 T,参与人 2 的任意策略 (q, 0, 0, 1-q) 都是一个最佳响应,其对应的收益都是 2 = 2q + 2(1-q),而这并不比纯策略 W 或 Z 的收益更高。但是,\{(T, (q,0,0,1-q)) \mid 0 < q < 1\} 中的每一个策略组合也都是该博弈的纳什均衡,你能说出为什么吗?
从这个例子中我们还可以看到,纳什均衡策略并不一定会带来帕雷托最优(Pareto optimal)收益。如果收益组合 (a, b) 和 (a',b') 满足 a' \geq a, b' > b 或者 a' > a, b' \geq b,则称 (a',b') 是 (a,b) 的帕雷托改进。如果 (a,b) 不存在帕雷托改进,则称其为帕雷托最优。策略组合 (M,Y) 的收益 (4,4) 是纳什均衡 (T,W) 的收益 (2,2) 的帕雷托改进,因此 (2,2) 不是帕雷托最优。这个现象我们在 Section 1.3.2 的囚徒困境博弈中也曾观察到。
3.2.2 2 \times 2 博弈
在这一节中我们通过一个例子展示如何用图形分析法解 2\times 2 博弈。考虑下面的双矩阵博弈
\begin{align*} & \ \ \ \ \, \begin{matrix} L & \ \ \, R \end{matrix} \\ \begin{matrix} T \\ B\end{matrix} & \begin{pmatrix} 2,2 & 0,1 \\ 1,1 & 3,3 \end{pmatrix} \end{align*}
注意这个博弈存在两个纯策略纳什均衡:(T,L) 和 (B,R)。下面我们尝试寻找所有的纳什均衡。
首先假设参与人 2 的策略是 (q, 1-q)。此时,如果参与人 1 的策略 T 的收益高于 B 的收益,那么它也高于任何混合策略 (p,1-p) 的收益,从而使 T 成为 (q, 1-q) 的最佳响应。因此,T 成为最佳响应的条件是
2q + 0(1-q) > 1q + 3(1-q) \ , 即 q > \tfrac{3}{4}。用同样的方法可知,B 成为最佳响应的条件是 q < \tfrac{3}{4}。而当 q=\tfrac{3}{4} 时,任意混合策略 (p, 1-p) 都是最佳响应。综上所述,如果我们将 (q, 1-q) 的最佳响应策略集合写成函数 \beta_1(q, 1-q),则有
\beta_1(q, 1-q) = \begin{cases} \{(1,0)\} & \text{ if } \tfrac{3}{4} < q \leq 1 \\ \{(p, 1-p) \mid 0 \leq p \leq 1\} & \text{ if } q = \tfrac{3}{4} \\ \{(0,1)\} & \text{ if } 0 \leq q < \tfrac{3}{4} \end{cases}
同理,针对参与人 1 的策略 (p, 1-p) 的最佳响应策略集合 \beta_2(p, 1-p) 可以写成
\beta_2(p, 1-p) = \begin{cases} \{(1,0)\} & \text{ if } \tfrac{2}{3} < p \leq 1 \\ \{(q, 1-q) \mid 0 \leq q \leq 1\} & \text{ if } p = \tfrac{2}{3} \\ \{(0,1)\} & \text{ if } 0 \leq p < \tfrac{2}{3} \end{cases}
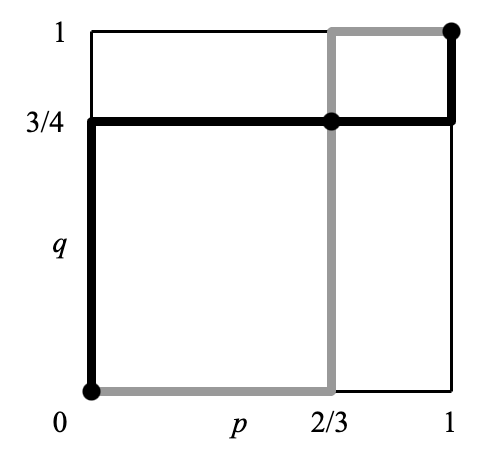
根据定义,纳什均衡 \boldsymbol{p}^*, \boldsymbol{q}^* 应满足 \boldsymbol{p}^* \in \beta_1(\boldsymbol{q}^*) 和 \boldsymbol{q}^* \in \beta_2(\boldsymbol{p}^*),即两个最佳响应函数的交点。画出两个函数 \beta_1(q, 1-q) 和 \beta_2(p, 1-p) 的图像即可轻松地找到这些交点。如果令横轴为 p,纵轴为 q,则函数图像如 Figure 3.1 所示。
黑色粗实线为参与人 1 的最佳响应函数,灰色粗实线为参与人 2 的最佳响应函数。二者的交点即为全部纳什均衡:((1,0), (1,0)), ((\tfrac{2}{3}, \tfrac{1}{3}), (\tfrac{3}{4}, \tfrac{1}{4})), ((0,1), (0,1))。
3.2.3 严格优势
在 Section 3.2.2 中我们将图形分析法应用在 2\times 2 博弈上,但它也可以应用在 2\times 3 或 3\times 2 博弈上,参考原书第十三章。
通常在寻找纳什均衡时,我们可以通过反复剔除严格劣势策略来降低博弈的维度。和 Chapter 2 一样,我们需要针对某一参与人找出严格劣势纯策略,然后将它们对应的行或列从矩阵中删除,然后在降维后的博弈中重复这一过程,直至没有新的严格劣势策略出现。在原书第十三章中证明了依此方法剔除的纯策略不会在任何纳什均衡中被选中(即概率为零),因此原博弈的纳什均衡策略不会被剔除。同时也不会出现原博弈中不存在的纳什均衡。另外剔除策略的顺序对结果不会产生影响。
考虑下面的双矩阵博弈
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ X & \ \ \,Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ M \\ B \end{matrix} & \begin{pmatrix} 2,2 & 2,1 & 2,2 & 0,0 \\ 1,0 & 4,1 & 2,4 & 1,5\\ 0,4 & 3,1 & 3,0 & 3,3 \end{pmatrix} \end{align*}
对于任意一个参与人,没有哪个纯策略是严格劣于另一个纯策略的。我们考虑参与人 2 的策略 X。通过观察可知,X 的收益低于 W 和 Y 的收益的最大值,即 1 < \max\{2,2\}, 1 < \max\{0,4\}, 1 < \max\{4,0\}。因此我们可以尝试找出严格优于 X 的 W 和 Y 的凸组合,即策略 (q,0,1-q,0)。我们需要的条件是
\begin{align*} 1 &< 2q + 2(1-q) \\ 1 &< 0q + 4(1-q) \\ 1 &< 4q + 0(1-q) \end{align*}
这三个不等式的解为 \tfrac{1}{4} < q < \tfrac{3}{4}。例如 X 严格劣于策略 (\tfrac{1}{2}, 0, \tfrac{1}{2}, 0)。因此我们可以删除策略 X,也就是矩阵的第二列。此时我们得到
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ M \\ B \end{matrix} & \begin{pmatrix} 2,2 & 2,2 & 0,0 \\ 1,0 & 2,4 & 1,5\\ 0,4 & 3,0 & 3,3 \end{pmatrix} \end{align*}
此时我们不难发现,当 \tfrac{1}{2} < p < \tfrac{2}{3} 时,参与人 1 的策略 M 严格劣于策略 (p, 0, 1-p)。因此我们可以删除第二行而得到更小的矩阵
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ Y & \ \ Z \end{matrix} \\ \begin{matrix} T \\ B \end{matrix} & \begin{pmatrix} 2,2 & 2,2 & 0,0 \\ 0,4 & 3,0 & 3,3 \end{pmatrix} \end{align*}
最后,Z 严格劣于 W,因此它可以被剔除。我们最终得到了一个 2\times 2 博弈
\begin{align*} & \ \ \ \ \ \begin{matrix} W & \ \ Y \end{matrix} \\ \begin{matrix} T \\ B \end{matrix} & \begin{pmatrix} 2,2 & 2,2 \\ 0,4 & 3,0 \end{pmatrix} \end{align*}
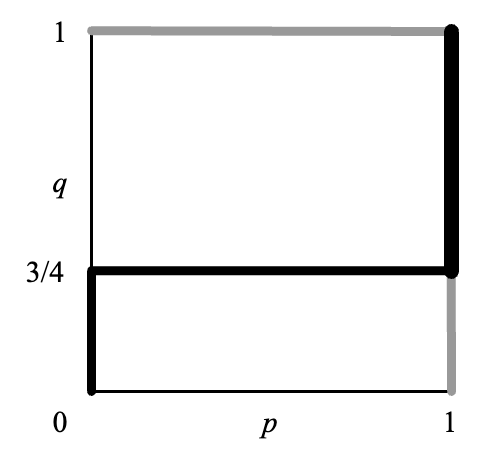
这个博弈可以用图形分析法求解,如 Figure 3.2 中所示。
加粗的黑色(灰色)折线代表参与人 1 (参与人 2)的最佳响应函数。在这个例子中,两者重叠的部分包含无穷多个点,即
\Big\{ \big( (1,0), (q,1-q) \big) \mid \tfrac{1}{3} \leq q \leq 1 \Big\} 这对应着原博弈中的纳什均衡
\Big\{ \big( (1,0,0), (q,0,1-q,0) \big) \mid \tfrac{1}{3} \leq q \leq 1 \Big\}