2 二人零和博弈

在本章中，我们讨论包含两个参与人的零和博弈（zero-sum game），即二人的（期望）收益之和永远为零的博弈。我们假设参与人拥有有限的纯策略（pure strategy）集合。Section 1.3.1 中的俾斯麦海海战博弈和猜硬币博弈属于这一分类。

在 Section 2.1 中我们将给出基本定义，在 Section 2.2 中学习如何使用剔除严格劣势策略（elimination of strictly dominated strategies）的方法解 2\times n、m \times 2 以及更大的博弈问题。

2.1 基本定义

有限二人零和博弈的所有数据都可以用一个矩阵来表达，因此我们也称该类博弈为矩阵博弈（matrix game）。

Definition 2.1 (矩阵博弈) 矩阵博弈是一个 m\times n 的实矩阵 A，其中 m 是行数，n 是列数。参与人 1 的（混合）策略是关于行的概率分布 \boldsymbol{p}，即下面集合的一个要素

\Delta^m := \big\{\boldsymbol{p} = (p_1, \dots, p_m) \in \mathbb{R}^m \mid \sum_{i=1}^m p_i = 1, p_i \geq 0 \text{ for all } i = 1, \dots, m \big\}

同样，参与人 2 的（混合）策略是关于列的概率分布 \boldsymbol{q}，即下面集合的一个要素

\Delta^n := \big\{\boldsymbol{q} = (q_1, \dots, q_n) \in \mathbb{R}^n \mid \sum_{j=1}^n q_j = 1, q_j \geq 0 \text{ for all } j = 1, \dots, n \big\}

参与人 1 的策略 \boldsymbol{p} 如果满足某一行 i 对应的 p_i = 1，则称该策略为纯策略（pure strategy），也可以写作 \boldsymbol{e}^i。同样，参与人 2 的纯策略满足某一列 j 对应的 q_j = 1，也可以写作 \boldsymbol{e}^j。

我们可以按照下述的方式理解矩阵博弈 A。如果参与人 1 选择行 i（即纯策略 \boldsymbol{e}^i），且参与人 2 选择列 j（即纯策略 \boldsymbol{e}^j），则参与人 1 获得的收益（payoff）为 A 的 (i,j) 要素 a_{ij}，参与人 2 需要支付 a_{ij}（获得收益为 - a_{ij}）。如果参与人 1 选择策略 \boldsymbol{p} 且参与人 2 选择策略 \boldsymbol{q}，则参与人 1 的期望收益为

\boldsymbol{p} A \boldsymbol{q} = \sum_{i=1}^m \sum_{j=1}^n p_i a_{ij} q_j ,

参与人 2 的期望收益为 -\boldsymbol{p} A \boldsymbol{q}。

Remark 2.1. (1) 根据 Definition 2.1，我们默认策略为混合策略，而纯策略是混合策略的特殊形式。当我们想强调纯策略时会加上修饰词“纯”。(2) 因为大多数情况下不会出现误解，所以我们没有标注矩阵的转置，例如 \boldsymbol{p}^\top \!A \boldsymbol{q}。

那么如何“解”矩阵博弈，即预测聪明的参与人会做出什么选择呢？我们这里用到的是 maximin 和 minimax 策略。首先我们给出定义

Definition 2.2 (maximin 和 minimax 策略) 策略 \boldsymbol{p} 如果满足下列条件，则称它为参与人 1 在矩阵博弈 A 中的 maximin 策略

\min\{\boldsymbol{p} A \boldsymbol{q} \mid \boldsymbol{q} \in \Delta^n\} \geq \min\{\boldsymbol{p}' A \boldsymbol{q} \mid \boldsymbol{q} \in \Delta^n\} \ \text{ for all } \boldsymbol{p}' \in \Delta^m

策略 \boldsymbol{q} 如果满足下列条件，则称它为参与人 2 在矩阵博弈 A 中的 minimax 策略

\max\{\boldsymbol{p} A \boldsymbol{q} \mid \boldsymbol{p} \in \Delta^m\} \leq \max\{\boldsymbol{p} A \boldsymbol{q}' \mid \boldsymbol{p} \in \Delta^m\} \ \text{ for all } \boldsymbol{q}' \in \Delta^n

也就是说，参与人 1 的 maximin 策略将自己的最小收益（由参与人 2 的策略导致）最大化，而参与人 2 的 minimax 将自己的最大支付（由参与人 1 的策略导致）最小化。因为策略集是有限的，maximin 策略和 minimax 策略永远存在。两个策略在定义上的区别自然是源于矩阵博弈中的数字对参与人 1 来说是收益，但对参与人 2 来说则是支付额。

如果要检验某个策略 \boldsymbol{p} 是否是参与人 1 的 maximin 策略，我们只需针对 \boldsymbol{e}^j, j = 1, 2, \dots, n 检验 Definition 2.2 中的第一个不等式是否成立即可，而不需要检验所有的 \boldsymbol{q} \in \Delta^n。这是因为任意的 \boldsymbol{p}A\boldsymbol{q} 都是 \boldsymbol{p}A\boldsymbol{e}^j 的线性组合，其最大值只会出现在某个 \boldsymbol{p}A\boldsymbol{e}^j。同样的逻辑也适用于参与人 2 的 minimax 策略。换句话说，检验 maximin 或 minimax 策略时，我们只需要考虑对方的纯策略。

为什么我们对这两个策略感兴趣？这两个策略看上去代表了一种非常保守或悲观的，假设最坏情况的态度。而支撑 maximin/minimax 策略的理由源自 minimax 定理：对任意矩阵博弈 A，存在一个实数 v=v(A) 并满足下面的条件

当且仅当策略 \boldsymbol{p} 是参与人 1 的 maximin 策略时，它可以保证参与人 1 至少可以获得收益 v。
当且仅当策略 \boldsymbol{q} 是参与人 2 的 minimax 策略时，它可以保证参与人 2 最多只需支付 v 给参与人 1。

因此，参与人 1 选择 maximin 策略时可以获得的最小收益是 v，参与人 2 选择 minimax 策略时可以获得的最小收益是 -v（需要支付的最大值为 v）。我们称这个 v=v(A) 为博弈 A 的值（value），且 maximin 策略和 minimax 策略分别是参与人 1 和 2 的最优策略。

“解”矩阵博弈意味着找出两个参与人的最优策略以及博弈的值。在 Section 1.3.1 的俾斯麦海海战博弈中，双方都选择纯策略北线时，盟军可以保证获得收益 2，日军可以保证支付 2，因此该博弈的值为 2，北线是双方的最优策略。这个例子中存在鞍点，即 a_{11} = 2，这使分析变得简单。

Definition 2.3 (鞍点) 矩阵博弈 A 中的 (i,j) 要素如果满足下面的条件，则称其为鞍点（saddle point）：

\begin{align*} & a_{ij} \geq a_{ij} \ \text{ for all } k = 1, \dots, m, \\ & a_{ij} \leq a_{ik} \ \text{ for all } k = 1, \dots, n, \end{align*}

即 a_{ij} 是在列 j 中是最大值，在行 i 中是最小值。

如果 (i,j) 是鞍点，则参与人 1 选择纯策略 i 即可保证至少获得收益 a_{ij}，而参与人 2 选择纯策略 j 可以保证最多支付 a_{ij}。因此 a_{ij} 就是矩阵博弈 A 的值 v(A)，\boldsymbol{e}^i 是参与人 1 的最优（maximin）策略，\boldsymbol{e}^j 是参与人 2 的最优（minimax）策略。

2.2 如何解 2\times n 博弈和 m \times 2 博弈

在这一节我们将看到如何解至少一个参与人具有两个策略的博弈。我们还将介绍严格优势的概念，以及利用它解矩阵博弈。

2.2.1 2\times n 博弈

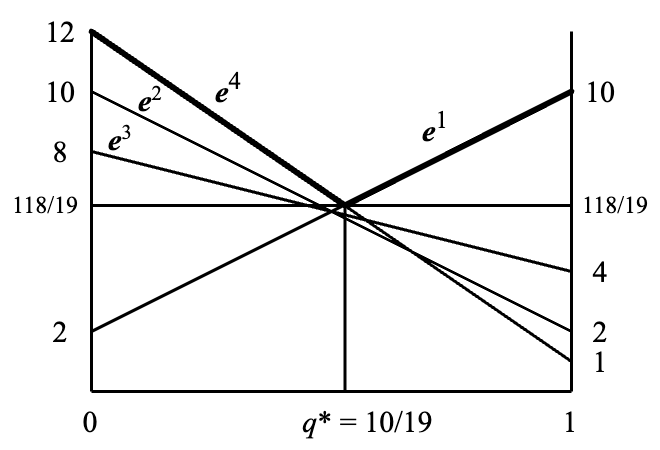
我们利用下面的例子展示如何利用图形解一个 2 行 n 列的矩阵博弈：

\begin{align*} & \begin{matrix} \,\boldsymbol{e}^1 & \,\boldsymbol{e}^2 & \,\boldsymbol{e}^3 & \,\boldsymbol{e}^4 \end{matrix} \\ A = \Bigg( & \begin{matrix} 10 \ & 2 \ & 4 \ & 1 \\ 2 \ & 10 \ & 8 \ & 12 \end{matrix} \Bigg) \end{align*}

我们已经对每一列（即参与人 2 的纯策略）进行了标注。令 \boldsymbol{p} = (p, 1-p) 为参与人 1 的任意策略。此时，针对参与人 2 的每一个纯策略，参与人 1 的期望收益是

\begin{align*} &\boldsymbol{p}A\boldsymbol{e}^1 = 10p + 2(1-p) = 8p+2 \\ &\boldsymbol{p}A\boldsymbol{e}^2 = 2p + 10(1-p) = 10-8p \\ &\boldsymbol{p}A\boldsymbol{e}^3 = 4p + 8(1-p) = 8-4p \\ &\boldsymbol{p}A\boldsymbol{e}^4 = p + 12(1-p) = 12-11p \end{align*}

我们将这四个关于 p 的线性函数画在同一张图中，可得 Figure 2.1。

图中的横轴为 p，四条细直线分别为参与人 2 的每个纯策略所对应的参与人 1 的期望收益。对每一个 0\leq p \leq 1 的取值，参与人 1 可获得的最小期望收益为图中的粗折线，也就是说对于任意的 p，参与人 2 的策略 (q_1, q_2, q_3, q_4) 是在该 p 位置上四条直线上的点的凸组合，而这一点一定是在粗折线上或者比粗折线高的位置上。很明显，粗折线上的最大值位于 p = p^* = \tfrac{1}{2}，其取值为 6。因此我们得到了参与人 1 的唯一最优（maximin）策略 \boldsymbol{p}^* = (\tfrac{1}{2}, \tfrac{1}{2})，而博弈值为 v(A) = 6。

那么参与人 2 的最优（minimax）策略是什么呢？从前一节我们知道，参与人 2 的 minimax 策略 \boldsymbol{q} = (q_1, q_2, q_3, q_4) 应当能够保证参与人 2 的支付额不超过博弈值。从 Figure 2.1 中可以看出 q_4 = 0，因为若非如此，参与人 1 的策略 (\tfrac{1}{2}, \tfrac{1}{2}) 对应的期望收益将大于 6，也就是说参与人 2 给参与人 1 的支付额将大于 6，而这不符合 minimax 策略的性质。因此参与人 2 的 minimax 策略应为 \boldsymbol{q} = (q_1, q_2, q_3, 0)。该策略是纯策略 \boldsymbol{e}^1, \boldsymbol{e}^2, \boldsymbol{e}^3 的线性组合，因此在图中对应着一条经过点 (\tfrac{1}{2}, 6) 的直线。由于 \boldsymbol{q} 是 minimax 策略，这条直线的最大值应该为 6。因此可知这条直线的斜率为 0。综合以上分析我们可以得到下面的条件

\begin{align*} 2q_1 + 10q_2 + 8q_3 &= 6 \qquad \text{左侧端点的位置是 } (0,6) \\ 10q_1 + 2q_2 + 4q_3 &= 6 \qquad \text{右侧端点的位置是 } (1,6) \\ q_1 + q_2 + q_3 &= 1 \qquad \boldsymbol{q} \text{ 是概率分布} \end{align*}

我们可以利用前两个等式消除 q_3 而将条件简化为

\begin{align*} 3q_1 - q_2 &= 1 \\ q_1 + q_2 + q_3 &= 1 \end{align*}

事实上我们只需要左右两个端点条件其中之一，因为我们已经知道该直线经过点 (\tfrac{1}{2}, 6)，而两点可以定义一条直线。

根据简化后的等式条件可知，参与人 2 的最优策略集合是

\big\{ \boldsymbol{q} = (q_1, q_2, q_3, q_4) \in \Delta^4 \mid q_2 = 3q_1 - 1, q_4 = 0 \big\}

从中可知当 q_1 = \tfrac{1}{3} 时 q_2 = 0，q_1 = \tfrac{1}{2} 时 q_2 = \tfrac{1}{2}。如果 q_1 < \tfrac{1}{3} 则 q_2 为负，反之如果 q_1 > \tfrac{1}{2} 则两者之和大于 1。因此参与人 2 的最优策略集合也可以写成

\big\{ \boldsymbol{q} = (q_1, q_2, q_3, q_4) \in \mathbb{R}^4 \mid \frac{1}{3} \leq q_1 \leq \frac{1}{2}, q_2 = 3q_1 - 1, q_3 = 1 - q_1 - q_2, q_4 = 0 \big\} 这说明参与人 2 的最优策略集合的维度为 1。

2.2.2 m \times 2 博弈

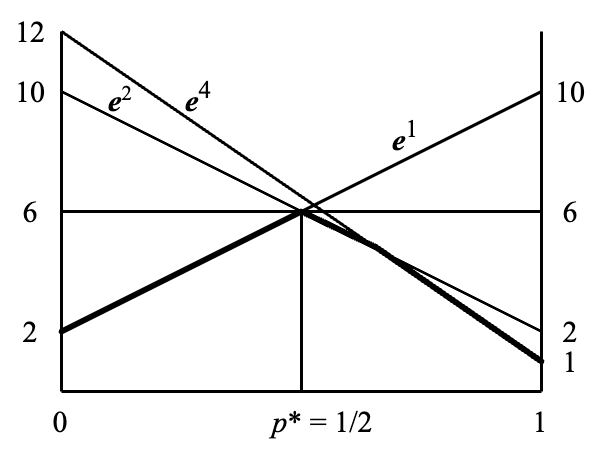
在这一节中我们用类似方法分析下面的博弈：

\begin{align*} A = \begin{matrix} \boldsymbol{e}^1 \\ \boldsymbol{e}^2 \\ \boldsymbol{e}^3 \\ \boldsymbol{e}^4 \end{matrix} \begin{pmatrix} 10 & 2 \\ 2 & 10 \\ 4 & 8 \\ 1 & 12 \end{pmatrix} \end{align*}

这是 Section 2.2.1 中矩阵的转置。令 \boldsymbol{q} = (q, 1-q) 为参与人 2 的任意策略。我们继续用图形分析，只是这次横轴为 q，而 \boldsymbol{e}^1, \boldsymbol{e}^2, \boldsymbol{e}^3, \boldsymbol{e}^4 对应的直线是参与人 1 选择这些纯策略时的期望收益（是 q 的函数）。这些直线的定义是

\begin{align*} &\boldsymbol{e}^1 A\boldsymbol{q} = 10q + 2(1-q) = 8q+2 \\ &\boldsymbol{e}^2 A\boldsymbol{q} = 2q + 10(1-q) = 10-8q \\ &\boldsymbol{e}^3 A\boldsymbol{q} = 4q + 8(1-q) = 8-4q \\ &\boldsymbol{e}^4 A\boldsymbol{q} = q + 12(1-q) = 12-11q \end{align*}

图形表达为 Figure 2.2。

此时，参与人 2 需要支付的最大值是图中的粗折线，其最小值发生在 \boldsymbol{e}^1 和 \boldsymbol{e}^4 的交点，即 (\tfrac{10}{19}, \tfrac{118}{19})。因此这个博弈的值为 \tfrac{118}{19}，参与人 2 的唯一最优（minimax）策略是 \boldsymbol{q}^* = (\tfrac{10}{19}, \tfrac{9}{19})。

从图中也可以看出，参与人 1 的最优策略 \boldsymbol{p} = (p_1, p_2, p_3, p_4) 是 \boldsymbol{e}^1 和 \boldsymbol{e}^4 的凸组合，即 p_2 = p_3 = 0，因为若非如此，该策略就无法保证参与人 1 的收益至少为博弈值 \tfrac{118}{19}，也就不是 maximin 策略。最优策略对应的直线应不小于 \tfrac{118}{19}，因此其斜率为 0。由此我们可以得到下面的条件

\begin{align*} 2p_1 + 12p_4 &= \tfrac{118}{19} \\ 10p_1 + p_4 &= \tfrac{118}{19} \\ p_1 + p_4 &= 0 \end{align*}

这个方程组有唯一解 (p_1, p_4) = (\tfrac{11}{19}, \tfrac{8}{19})。因此，参与人 1 的最优（maximin）策略是 \boldsymbol{p}^* = (\tfrac{11}{19}, 0, 0, \tfrac{8}{19})。

2.2.3 严格优势（strict domination）

我们可以用剔除严格劣势的纯策略这种方法简化图形分析的复杂度。考虑下面的博弈

\begin{align*} & \begin{matrix} \,\boldsymbol{e}^1 & \,\boldsymbol{e}^2 & \,\boldsymbol{e}^3 & \,\boldsymbol{e}^4 & \boldsymbol{e}^5 \end{matrix} \\ A = \Bigg( & \begin{matrix} 10 \ & 2 \ & 5 \ & 1 & \ 6\\ 2 \ & 10 \ & 8 \ & 12 & \ 9 \end{matrix} \Bigg) \end{align*}

在这个博弈中，参与人 2 的最优策略中 \boldsymbol{e}^5 的比例应为 0，因为无论参与人 1 如何选择，\boldsymbol{e}^3 的收益永远高于 \boldsymbol{e}^5。我们说 \boldsymbol{e}^5 严格劣于（strictly dominated by） \boldsymbol{e}^3，因此选择它的概率为零。这是一个纯策略严格劣于另一个纯策略的例子。

一个纯策略也可能严格劣于一个混合策略。现在我们考虑 \boldsymbol{e}^3。它在第一行的支付 5 介于 \boldsymbol{e}^1 和 \boldsymbol{e}^2 在第一行的支付 10 和 2 之间，而它在第二行的支付 8 也是介于 \boldsymbol{e}^1 和 \boldsymbol{e}^2 在第二行的支付 2 和 10 之间，因此有可能存在一种 \boldsymbol{e}^1 和 \boldsymbol{e}^2 的组合能够严格优于 \boldsymbol{e}^3。为了找到这种组合，我们假设选择 \boldsymbol{e}^1 和 \boldsymbol{e}^2 的概率为 (\alpha, 1-\alpha)，则

\alpha \begin{pmatrix} 10 \\ 2 \end{pmatrix} + (1-\alpha) \begin{pmatrix} 2 \\ 10 \end{pmatrix} = \begin{pmatrix} 8\alpha + 2 \\ 10 - 8\alpha \end{pmatrix}

我们希望 \alpha 满足 8\alpha + 2 < 5 和 10-8\alpha < 8，而这两个不等式的解为 \tfrac{1}{4} < \alpha < \tfrac{3}{8}。因此在这个范围内 \boldsymbol{e}^3 严格劣于混合策略 (\alpha, 1-\alpha, 0,0,0)。这说明在参与人 2 的最优策略中，选择 \boldsymbol{e}^3 的概率 q_3=0，因为若非如此，参与人 2 可以通过将 \alpha q_3 分配给 \boldsymbol{e}^1、将 (1-\alpha) q_3 分配给 \boldsymbol{e}^2 的方式使自己支付得更少（对任意 \tfrac{1}{4} < \alpha < \tfrac{3}{8} 成立）。

从以上分析可见，在解这个博弈之前我们可以将 \boldsymbol{e}^3 和 \boldsymbol{e}^5 剔除。因此在进行图形分析时，我们可以不考虑 \boldsymbol{e}^3 和 \boldsymbol{e}^5 对应的直线，见 Figure 2.3。此时博弈值是 6，参与人 1 的最优策略依然 \boldsymbol{p}^* = (\tfrac{1}{2}, \tfrac{1}{2})，参与人 2 的最优策略是 \boldsymbol{p}^* = (\tfrac{1}{2}, \tfrac{1}{2}, 0,0,0)。

在任何情况下，矩阵博弈中的严格劣势纯策略都不会以正概率的形式出现在任何最优策略中，因此我们可以在解之前将其剔除。有时这个做法也可以用在两个参与人都拥有两个以上策略的博弈中（即 m,n>2）。另外，剔除严格劣势策略也可以反复进行，即在剔除原博弈中所有的严格劣势策略后，新产生的（更小的）博弈中也可能出现新的严格劣势策略，此时我们可以继续剔除，直至没有新的严格劣势策略出现，见 Example 2.1。原书第十三章中有更加严密的证明可以参考。

下面我们给出严格劣势的定义，然后分析 Example 2.1。

Definition 2.4 (严格优势，strict domination) 令 A 为 m \times n 的矩阵博弈，i 为其中的一行。纯策略 \boldsymbol{e}^i 如果满足下列条件，则称其为严格劣势（strictly dominated）策略

\exists \, \boldsymbol{p} \in \Delta^m \ \mathrm{ s.t. } \ \boldsymbol{p} A \boldsymbol{e}^j > \boldsymbol{e}^i A \boldsymbol{e}^j \ \text{ for every } j = 1, \dots, n

同样，令 j 为 A 中的一列。纯策略 \boldsymbol{e}^j 满足下列条件时为严格劣势策略

\exists \, \boldsymbol{q} \in \Delta^n \ \mathrm{ s.t. } \ \boldsymbol{e}^i A \boldsymbol{q} < \boldsymbol{e}^i A \boldsymbol{e}^j \ \text{ for every } i = 1, \dots, m

从定义可知，严格优势（或严格劣势）是一个基于收益向量间的比较的概念。当收益向量 \boldsymbol{a} > \boldsymbol{b} 时，我们说 \boldsymbol{a} 对应的策略严格优于（strictly dominates） \boldsymbol{b} 对应的策略，反过来 \boldsymbol{b} 对应的策略严格劣于（strictly dominated by） \boldsymbol{a} 对应的策略。而在应用时，往往用到的只是（剔除）严格劣势策略。

Remark 2.2. 不难发现，如果 \boldsymbol{e}^i 严格劣于策略 \boldsymbol{p}，则 p_i = 0。同样，如果 \boldsymbol{e}^j 严格劣于策略 \boldsymbol{q}，则 q_j = 0。

Example 2.1 考虑下面的 3\times 3 矩阵博弈

A = \begin{pmatrix} 6 & 0 & 2 \\ 0 & 5 & 4 \\ 3 & 2 & 1 \end{pmatrix}

参与人 1 的策略 \boldsymbol{e}^3 严格劣于策略 \boldsymbol{p} = (\tfrac{7}{12}, \tfrac{5}{12}, 0)，因为

\boldsymbol{p}A = (\begin{matrix} \tfrac{7}{2} & \tfrac{25}{12} & \tfrac{17}{6} \end{matrix}) > \boldsymbol{e}^3A = (\begin{matrix} 3 & 2 & 1 \end{matrix})

因此参与人 1 在任何最优策略中选择第三行的概率都为零。从矩阵 A 中删除第三行可得

B = \begin{pmatrix} 6 & 0 & 2 \\ 0 & 5 & 4 \end{pmatrix}

这时，参与人 2 的策略 \boldsymbol{e}^3 严格劣于策略 \boldsymbol{q} = (\tfrac{1}{4}, \tfrac{3}{4}, 0)，因为

B\boldsymbol{q} = \begin{pmatrix} \tfrac{3}{2} \\ \tfrac{15}{4} \end{pmatrix} < B\boldsymbol{e}^3 = \begin{pmatrix} 2 \\ 4 \end{pmatrix}

因此参与人 2 在任何最优策略中选择第三列的概率都为零。从矩阵 B 中删除第三列可得

C = \begin{pmatrix} 6 & 0 \\ 0 & 5 \end{pmatrix}

C 是一个 2 \times 2 矩阵博弈，你能找到它的解吗？