4 扩展式博弈
大多数从现实的经济和政治现象引申出的博弈问题都和棋牌类游戏有着共同点,即它们都不是单次博弈,参与人按照一定顺序选择行动,且同一个参与人往往会有多次行动的机会。这类博弈最好以决策树的形式表达,这样可以明确参与人的行动顺序,以及在行动时该参与人了解哪些信息。
在本章中我们学习这类扩展式博弈(games in extensive form)。我们只讨论有限参与人(一般为两人),有限决策回合,以及有限行动集的博弈,参见 Section 1.3.3 中展示的例子。我们也假设每个参与人都拥有完全信息(complete information),即博弈中不存在随机选择,或即使存在随机选择也是在所有参与人完成选择之后,且随机选择的结果不公开。这不包括 Section 1.3.3 中的不完全信息下的市场进入与威慑博弈,也不包括大部分以分牌开始的棋牌类游戏(分牌的过程可以视作随机选择)。我们将在 Chapter 5 学习不完全信息博弈。原书第十四章在这两章的基础上进行了扩展。
在第一节中我们将定义扩展式博弈。为了避免使用过于复杂的符号,这一节中的定义会有些不正式,但依然是准确的。在 Section 4.2 中我们将定义策略以及策略式博弈(games in strategic form)1。扩展式博弈的纳什均衡可以通过其对应的策略式博弈求得。在这一节中我们只专注于求纯策略纳什均衡。
1 也称为标准式博弈(normal form game)。
2 在博弈论中,精炼(refinement)一词的数学含义是通过加入更多的限制条件使集合包含的要素变得更少。精炼后的纳什均衡比原始定义包含更少的策略组合,可以提供更好的预测或排除不合理的策略。
在第三节中,我们将通过使用逆向归纳法和附加子博弈完美性的方式精炼(refine)纳什均衡2。作为更进一步精炼的完美贝叶斯均衡将在第四节中介绍。
4.1 扩展式博弈
扩展式博弈由一个博弈树(game tree)表达。博弈树由节点(node)和边(edge)组成。节点可以表达下列内容之一:参与人的决策点(decision node),随机选择的决策点(chance node),博弈的终点(end node)。边可以代表参与人或随机选择的一个行动(action)。随机选择有时也被称作自然(Nature)的选择3。
3 自然(Nature)是一个假想的特殊参与人,它和普通参与人一样可以选择行动,但要服从给定的概率分布。
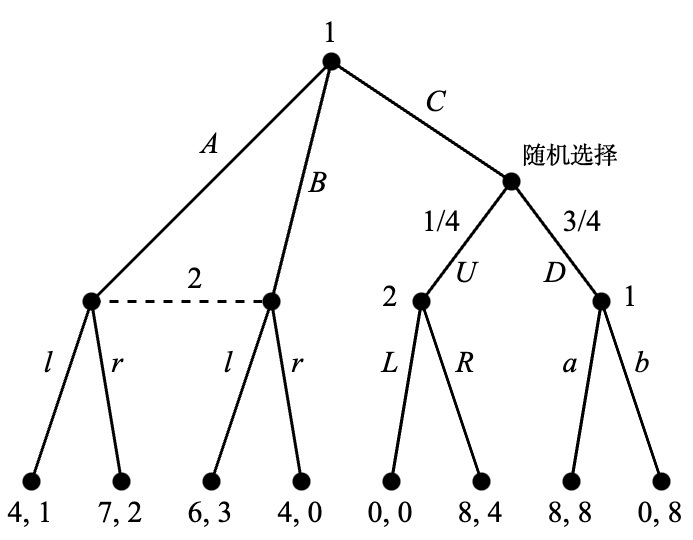
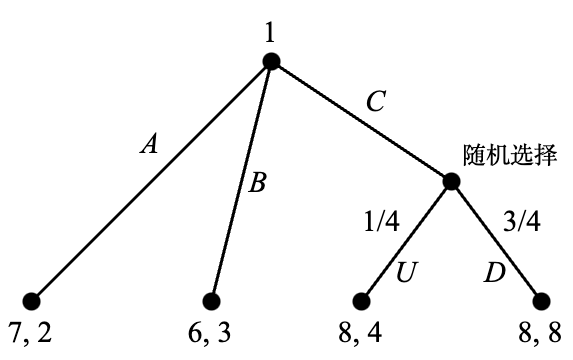
Figure 4.1 展示了一个扩展式博弈的博弈树。
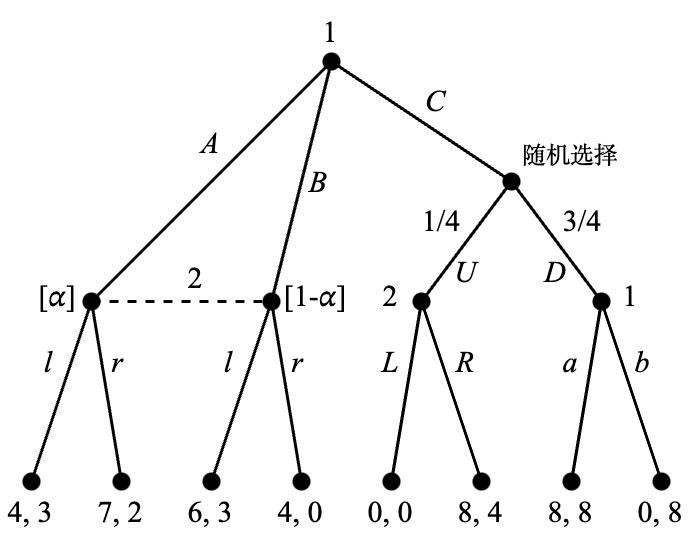
博弈树中最顶端的节点称为根(root)是整个博弈的起始点。在这个例子中,根是参与人 1 的决策节点,他需要在行动 A, B, C 中进行选择。参与人 2 在下一回合进行决策时知道参与人 1 是选择了 A 和 B 其中之一,或者选择了 C。但是参与人 2 无法区分 A 和 B,这在图中以虚线连接两个节点的形式表达,被连接的两个节点形成了一个信息集(information set)。在这个信息集上,参与人 2 有两个选择,即 \ell 和 r。注意参与人在同一信息集中的每个节点上的备选行动集是相同的,若果不相同则代表该参与人能够分清自己位于哪个节点上,这违反了信息集的含义。而在一切背后还有一个隐藏的前提条件:整个博弈树是所有参与人的共同知识(common knowledge)。共同知识这个概念比它的字面意思更加复杂,它意味着每个参与人都知道其内容,且每个参与人都知道“每个参与人都知道其内容”这件事,且每个参与人都知道“每个参与人都知道‘每个参与人都知道其内容’”这件事,依此类推直至无穷。
如果参与人 1 选择了 C,则接下来有一个随机选择:以 1/4 的概率选择 U 并让参与人 2 继续决策,或以 3/4 的概率选择 D 并让参与人 1 继续决策。在参与人 2 的决策节点上有两个行动 L 和 R,而在参与人 1 的决策节点上也有两个行动 a 和 b。所有剩余的节点都是终点,每个终点对应一组收益。
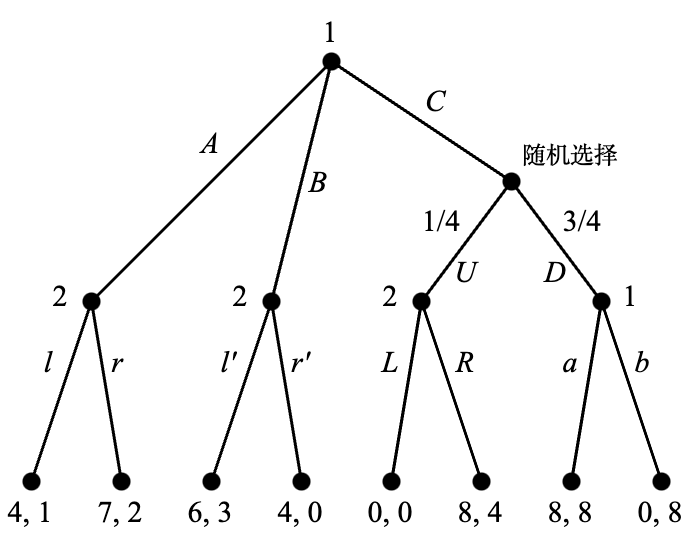
需要注意的是,每一个单独的决策节点(不以虚线和其他节点连接)也是一个信息集。因此,这个博弈中有两种信息集,我们称含有至少两个节点的信息集为非平凡(nontrivial)的。含有非平凡信息集的博弈称为不完美信息博弈(games with imperfect information),反之只含有平凡信息集的博弈称为完美信息博弈(games with perfect information)。如果我们假设上面的例子中参与人 2 可以观察到参与人 1 究竟是选择了 A 还是 B,就可以得到一个完美信息博弈,见 Figure 4.2。为了反映参与人 2 可以区分参与人 1 的行动 A 和 B,这里将 B 之后的参与人 2 的行动改名为 \ell' 和 r'。
这个博弈中的随机选择并不具有特殊意义,因为其他参与人可以知道随机选择的结果。如果至少一个参与人无法完全知晓随机选择的结果,且会因此影响到自己的决策,那么我们就拥有了一个不完全信息博弈,见 Chapter 5。
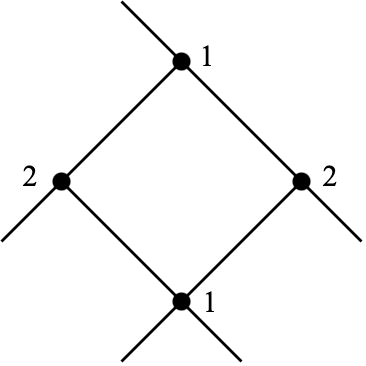
Figure 4.1 和 Figure 4.2 中的例子包含了扩展式博弈的主要要素,但并没有给出正式定义4。这里最重要的一点是博弈树必须满足树(tree)的数学性质:仅存在一个根,并且不包含环(cycle)。Figure 4.3 中给出了一个环的例子,而博弈树中不应该包含这样的部分。
4 原书第十四章中正式定义了扩展式博弈。
5 关于完美记忆的假设在区分混合策略和行为策略(behavioral strategy)时将变得十分重要,见原书第十四章。
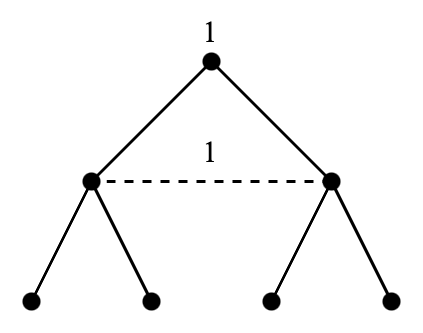
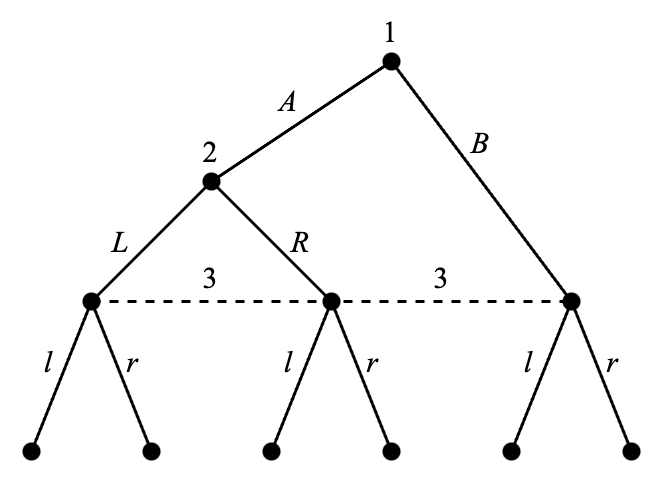
我们还要求扩展式博弈具有完美记忆(perfect recall):每个参与人都记得自己曾经作出的所有决策。例如在 Figure 4.4 中,参与人 1 位于下方的信息集时就不记得之前的决策结果,他分不清自己究竟是在左边的节点还是在右边的节点,这样的博弈我们不予讨论5。
4.2 策略式博弈
在扩展式博弈中,明确区分行动(action)和策略(strategy)十分重要。行动指参与人在位于每个信息集上时可以选择的备选项。例如在 Figure 4.1 中参与人 1 可选的行动包括 A, B, C 和 a, b;参与人 2 可选的行动包括 \ell, r 和 L, R。相比之下,
这是博弈论中最重要的概念之一。在 Figure 4.1 和 Figure 4.2 中,参与人 1 的策略可以是
或者
后者看上去可能有些奇怪,因为参与人 1 的第一个选择将导致他不会有第二次选择的机会。但尽管如此,这个行动计划也被认为是可行的6。
6 当然,如果我们禁止这样的策略也不会损失什么。有些作者就是这样做的。
Figure 4.1 中参与人 2 的策略可以是
注意参与人 2 无法针对参与人 1 的行动 A 和 B 分别选择对应的行动,因为他不掌握准确信息。但是在 Figure 4.2 的完美信息博弈中,参与人 2 的策略则应该区分 A 和 B 的两种情形,例如一种可能的策略是
策略的正式定义如下:
在上面的例子中,参与人 1 有两个信息集,因此他的策略应包含两个行动。他的备选策略的总数等于可能的行动清单的数量。参与人 1 在第一个信息集中有三个备选行动,而在第二个信息集中有两个备选行动,因此他总共有 3 \times 2 = 6 个备选策略。参与人 1 的策略集合为
\{ Aa, Ab, Ba, Bb, Ca, Cb \}
策略也可以用有序集合的形式表达,例如 \{A, a\},但是这显得冗长。在不产生误解的前提下,我们更倾向于使用简化形式 Aa。
与此类似,在 Figure 4.1 的不完美信息博弈中,参与人 2 的策略集合为
\{\ell L, \ell R, rL, rR \}
而在 Figure 4.2 的完美信息博弈中,参与人 2 有三个信息集,每个信息集各有两个备选行动,因此他有 2\times 2 \times 2 = 8 个备选策略。其策略集合为
\{ \ell \ell' L, \ell \ell' R, \ell r' L, \ell r' R, r \ell' L, r \ell' R, r r' L, r r' R \}
通常我们需要区分策略组合和它对应的结果(outcome)。结果是由策略组合决定的在博弈树上的行进路径。例如,在 Figure 4.2 中,策略组合 (Aa, \ell \ell' L) 对应的结果是 (A, \ell),收益向量是 (4, 1)。
为什么我们更关注策略而不是其他概念?首要原因是当我们考虑策略时,扩展式博弈可以简化为一个单次博弈。当我们确定一组策略的组合时,我们可以根据它决定的博弈树上的行进路径计算收益。让我们看一下 Figure 4.1 中的策略组合 (Cb, rL) 。参与人 1 首先选择 C,随后是随机选择。如果随机选择的结果是 U 则参与人 2 选择 L;如果是 D 则参与人 1 选择 b。因此两个参与人有 \tfrac{1}{4} 的概率获得收益 (0,0),有 \tfrac{3}{4} 的概率获得收益 (0,8)。参与人 1 的期望收益是 0,而参与人 2 的期望收益则是 6。用这样的方法可以计算 Figure 4.1 中所有 6 \times 4 = 24 个策略组合对应的期望收益向量。同样,在 Figure 4.2 中我们有 6 \times 8 = 48 组收益向量。接下去我们可以将这些收益向量写成双矩阵,如下所示:
\begin{align*} & \ \ \ \ \,\begin{matrix} \ell L & \ \ell R & \ rL & \ rR \end{matrix} \\ \begin{matrix} Aa \\ Ab \\ Ba \\ Bb \\ Ca \\ Cb \end{matrix} & \begin{pmatrix} 4,1 & 4,1 & \underline{7},\underline{2} & {7},\underline{2} \\ 4,1 & 4,1 & \underline{7},\underline{2} & {7},\underline{2} \\ \underline{6},\underline{3} & {6},\underline{3} & 4,0 & 4,0 \\ \underline{6},\underline{3} & {6},\underline{3} & 4,0 & 4,0 \\ \underline{6},{6} & \underline{8},\underline{7} & 6,6 & \underline{8},\underline{7} \\ 0,6 & 2,\underline{7} & 0,6 & 2,\underline{7} \end{pmatrix} \end{align*}
\begin{align*} & \ \ \ \begin{matrix} \ell \ell' L & \ell \ell' R & \ \ell r' L & \, \ell r' R & r \ell' L & \ r \ell' R & r r' L & \, r r' R \end{matrix} \\ \begin{matrix} Aa \\ Ab \\ Ba \\ Bb \\ Ca \\ Cb \end{matrix} & \begin{pmatrix} 4,1 \ \ & 4,1 \ \ & 4,1 \ \ & 4,1 \ \ & \underline{7},\underline{2} \ \ & {7},\underline{2} \ \ & \underline{7},\underline{2} \ \ & {7},\underline{2}\\ 4,1 \ \ & 4,1 \ \ & 4,1 \ \ & 4,1 \ \ & \underline{7},\underline{2} \ \ & {7},\underline{2} \ \ & \underline{7},\underline{2} \ \ & {7},\underline{2}\\ \underline{6},\underline{3} \ \ & {6},\underline{3} \ \ & 4,0 \ \ & 4,0 \ \ & {6},\underline{3} \ \ & {6},\underline{3} \ \ & 4,0 \ \ & 4,0 \\ \underline{6},\underline{3} \ \ & {6},\underline{3} \ \ & 4,0 \ \ & 4,0 \ \ & {6},\underline{3} \ \ & {6},\underline{3} \ \ & 4,0 \ \ & 4,0 \\ \underline{6},{6} \ \ & \underline{8},\underline{7} \ \ & \underline{6},6 \ \ & \underline{8},\underline{7} \ \ & {6},{6} \ \ & \underline{8},\underline{7} \ \ & 6,6 \ \ & \underline{8},\underline{7} \\ 0,6 \ \ & 2,\underline{7} \ \ & 0,6 \ \ & 2,\underline{7} \ \ & 0,6 \ \ & 2,\underline{7} \ \ & 0,6 \ \ & 2,\underline{7} \end{pmatrix} \end{align*}
这样表达出来的双矩阵博弈称为扩展式博弈的策略式(strategic form)表达。扩展式博弈的纳什均衡即可定义为
此定义适用于纯策略和混合策略,但是在本章中我们只讨论纯策略以及纯策略纳什均衡。
上面的双矩阵博弈中的纯策略纳什均衡可以用 Section 3.2.1 中的方法找出。Figure 4.1 中的不完全信息博弈有 6 个纯策略纳什均衡,而 Figure 4.2 中的完全信息博弈有 10 个纯策略纳什均衡。
在下一节中我们进一步学习这些纳什均衡,并讨论如何区分它们。
4.3 逆向归纳法和子博弈完美性
我们首先考虑 Figure 4.2 中的完美信息博弈。这个博弈可以用逆向归纳法分析。首先我们将每一个终点前的决策节点替换成终点,此时的收益为原来该节点上的最优行动带来的收益。例如参与人 2 在参与人 1 选择 A 之后的决策节点上应当选择 r,在 B 之后应当选择 \ell',在 C 和随机决策 U 之后应当选择 R。而参与人 1 在随机决策 D 之后应当选择 a。这样我们就得到了简化的博弈 Figure 4.5。在这一步之后,我们已经可以确定参与人 2 的策略为 r \ell' R,而参与人 1 在自己的第二个信息集处选择 a。注意在简化博弈中只剩下参与人 1 (和随机选择)。下一步就是在简化博弈中通过比较期望收益确定参与人 1 的最优行动。参与人 1 选择 A 的收益是 7,选择 B 的收益是 6,而选择 C 的期望收益是 8。因此参与人 1 此时的最优行动是 C。综上所述,我们得到了策略组合 (Ca, r\ell' R),其对应的期望收益组合是 \tfrac{1}{4}(8,4) + \tfrac{3}{4}(8,8) = (8,7)。从上一节可知,这是一个纯策略纳什均衡,这里称作逆向归纳均衡(backward induction equilibrium)。
可以证明在完美信息博弈中,应用逆向归纳法总是会得到一个纯策略纳什均衡。因此,完美信息博弈拥有至少一个纯策略纳什均衡,并可以通过逆向归纳法计算。
值得强调的是,我们应当考虑逆向归纳均衡而不是它对应的结果。在这个例子中,前者为策略组合 (Ca, r\ell' R),而后者是它对应的博弈树上的路径 (Ca, R)。除了逆向归纳均衡以外,还有三个纳什均衡也对应着同样的结果,它们是 (Ca, \ell \ell' R),(Ca, \ell r' R) 和 (Ca, r r' R)。在这三个纳什均衡中,参与人 2 在博弈树的左半边都选择了非最优行动7。因此,逆向归纳均衡可以保证每个参与人在任何位置都会选择最优行动,特别是在博弈路径以外的部分。
7 但并没有影响最终的收益,因为这些非最优行动发生在博弈路径之外的信息集上。
子博弈完美性(subgame perfection)是逆向归纳法的一般化。首先我们定义子博弈。
8 仅包含一个决策节点的信息集。
Figure 4.6 很好的诠释了 Definition 4.2 的后一半。虽然参与人 2 的决策节点是平凡信息集,但是从此处无法形成子博弈,因为它下面的(参与人 3)的决策节点所在的信息集包含了外部节点(即参与人 1 选择 B 之后的决策节点)。更加直观的解释是,参与人 3 无法观察任何前面的决策结果,也就不知道自己是否在由参与人 2 的决策节点开始的子树上。
Figure 4.2 包含六个不同的子博弈:即原博弈整体,由随机选择节点开始的子博弈,由终点前的四个节点开始的子博弈。下面我们给出子博弈完美均衡的定义。
让我们通过 Figure 4.2 验证一下此定义的含义。在确认一个策略组合是否是子博弈完美均衡时,我们需要针对每个子博弈进行验证。因为原博弈永远是自身的一个子博弈,因此子博弈完美均衡必须是原博弈的一个纳什均衡,也就是说 Figure 4.2 的子博弈完美均衡是其 10 个纳什均衡中的一个。这个结论具有一般性,因此可以说任意子博弈完美均衡也是纳什均衡。
接下来我们验证四个由终点的前一个节点开始的子博弈。这四个子博弈都只包含一个参与人,因此也称为单人博弈(one-person game)9。虽然我们没有定义单人博弈的纳什均衡,但其唯一合理的定义应该就是参与人永远选择最优行动。在这个例子中,这意味着在这四个子博弈里,参与人应当分别(从左到右)选择 r, \ell', R 和 a。而这同时也意味着在由随机选择节点开始的子博弈中,参与人们也作出了最优选择10。综合以上信息可知,我们需要能够在最后的决策节点实现 r, \ell', R, a 的纳什均衡,而满足条件的唯一策略组合是 (Ca, r \ell' R)。因此,(Ca, r \ell' R ) 是此博弈中唯一的子博弈完美均衡。同时我们观察到,在完美信息博弈中,逆向归纳均衡和子博弈完美均衡是一致的。
9 单人博弈问题其实就是单人决策问题,因此通常不放在博弈论的范畴内讨论。
10 随机选择本身是随机的,不是决策的结果,因此不存在优劣之分。
现在我们回到 Figure 4.1 中的不完美信息博弈。在这个例子中,逆向归纳法无法应用到博弈树的左半边,因为此处的参与人 2 的信息集包含两个节点,也就是说参与人 2 不知道之前参与人 1 的选择是 A 还是 B,因此也就无法选择最优行动:当参与人 1 选择 A 时则 r 更好,反之则 \ell 更好。而关于子博弈完美均衡,我们需要验证四个子博弈:原博弈整体,由随机选择节点开始的子博弈,U 下面的子博弈,D 下面的子博弈。因此,子博弈完美性要求参与人 1 选择 a 而参与人 2 选择 R,同时需是原博弈的纳什均衡。原博弈的 6 个纳什均衡中,满足此条件的是 (Ca, \ell R) 和 (Ca, rR),因此它们是子博弈完美均衡。
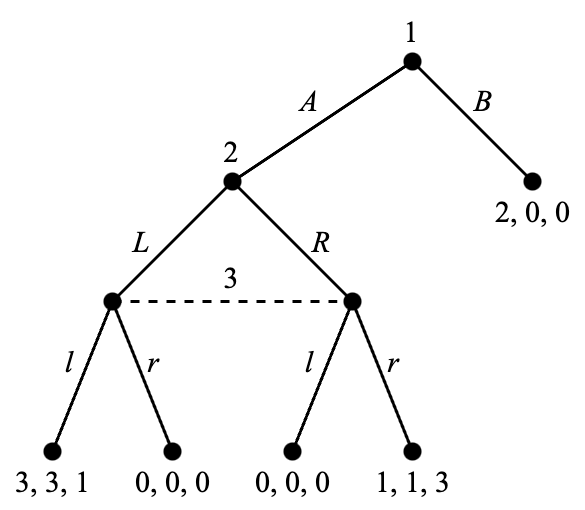
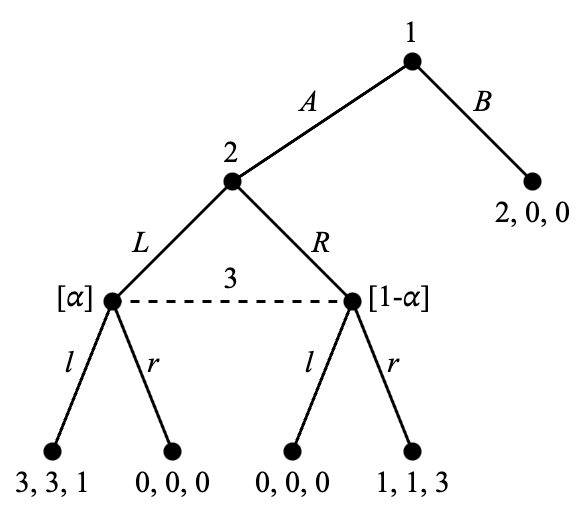
在本节的最后,我们用一个更清晰的例子说明子博弈完美均衡比逆向归纳均衡的适用范围更广。考虑 Figure 4.7 中的三人博弈。由于参与人 3 无法作出最优选择,我们无法应用逆向归纳法。关于子博弈完美均衡,我们要讨论两个子博弈:原博弈和由参与人 2 的决策节点开始的子博弈。后者是参与人 2 和参与人 3 之间的博弈,其策略式表达是
\begin{align*} & \ \ \ \ \ \begin{matrix} \ell & \ \ \ \ r \end{matrix} \\ \begin{matrix} L \\ R \end{matrix} & \begin{pmatrix} 3,1 & 0,0 \\ 0,0 & 1,3 \end{pmatrix} \end{align*}
这里参与人 2 是行参与人,参与人 3 是列参与人。这个博弈有两个纯策略纳什均衡:(L, \ell) 和 (R, r)。因此,子博弈完美均衡需要在这个子博弈中形成这两个纳什均衡之一。我们可以注意到,为了形成 (L, \ell) 则参与人 1 需要选择 A,因为这会给自己带来收益 3,高于选择 B 带来的收益 2。为了形成 (R, r) 则参与人 1 需要选择 B,因为此时收益 2 高于选择 A 带来的收益 1。因此,两个子博弈完美均衡分别是 (A, L, \ell) 和 (B, R, r)。
另一种方法是首先找出原博弈的所有纯策略纳什均衡。原博弈的策略式表达可以写成两个三重矩阵
\begin{align*} & \ \ \ \ \ \ \ \begin{matrix} \ell & \ \ \ \ \ \ \ \ r \end{matrix} & & \ \ \ \ \ \ \ \begin{matrix} \ell & \ \ \ \ \ \ \ \ r \end{matrix} \\ 1 : A \quad \begin{matrix} L \\ R \end{matrix} & \begin{pmatrix} \underline{3},\underline{3},\underline{1} & 0,0,0 \\ 0,0,0 & 1,\underline{1},\underline{3} \end{pmatrix} & 1 : B \quad \begin{matrix} L \\ R \end{matrix} & \begin{pmatrix} 2,\underline{0},\underline{0} & \underline{2},\underline{0},\underline{0} \\ \underline{2},\underline{0},\underline{0} & \underline{2},\underline{0},\underline{0} \end{pmatrix} \end{align*}
其中左侧的矩阵为参与人 1 选择 A 时的情形,右侧的则对应 B。我们已经用下划线标出了最佳响应(针对参与人 1 需要比较两个矩阵中相同位置的收益)。纯策略纳什均衡是 (A, L, \ell),(B, L, r),(B, R, \ell) 和 (B, R, r)。其中符合子博弈完美条件的即为 (A, L, \ell) 和 (B, R, r),与之前的分析结果相同。
4.4 完美贝叶斯均衡
针对纳什均衡和子博弈完美均衡的进一步精炼是完美贝叶斯均衡(perfect Bayesian equilibrium, PBE)。在扩展式博弈的信息集中,在该信息集作决策的参与人的信念(belief)是针对该信息集所包含节点(或到达该信息集的行动)的概率分布。如果信息集是平凡的,则信念也是平凡的,这意味着赋予该节点以概率 1。完美贝叶斯均衡的(非正式)定义如下。
第一个条件说的是,只要可行,信念应当针对策略依照贝叶斯公式进行计算。第二个条件说的是,参与人应当根据自己的信念计算期望收益并进行最优化。如果你感觉看不懂,那是非常正常的。我们将通过几个例子展示这两个条件具体意味着什么,而更加正式的定义可以参考原书第十四章。
贝叶斯公式:
\mathrm{Pr}[P\mid Q] = \frac{\mathrm{Pr}[P] \times \mathrm{Pr}[Q \mid P]}{\mathrm{Pr}[Q]}
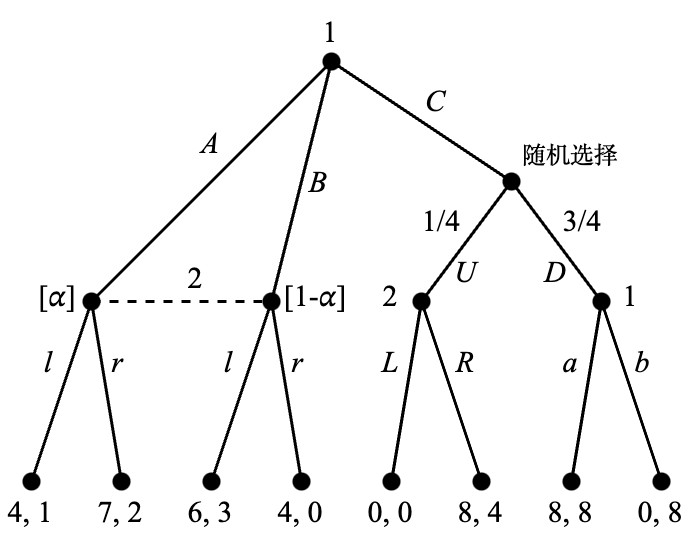
Figure 4.8 针对 Figure 4.1 中的博弈进行了一些补充。在参与人 2 的非平凡信息集中,信念 (\alpha, 1-\alpha) 现在被明确标注出来了。这意味着如果博弈进行到了这个信息集,则参与人 2 认为参与人 1 选择了 A 的概率为 \alpha,而选择了 B 的概率为 1-\alpha。所有其他信息集都是平凡的,因此对应的信念都是概率 1。条件 (2) 的序贯理性在这里意味着参与人 2 在 U 下面的信息集应当选择 R,参与人 1 在 D 下面的信息集应当选择 a。参与人 2 在他的非平凡信息集时应当基于信念最大化自身的期望收益:行动 \ell 的期望收益为 \alpha \cdot 1 + (1-\alpha)\cdot 3 = 3-2\alpha,行动 r 的期望收益为 \alpha \cdot 2 + (1-\alpha)\cdot 0 = 2\alpha,因此当 3-2\alpha \geq 2\alpha \Leftrightarrow 0 \leq \alpha \leq 3/4 时应选择 \ell,而在 3/4 \leq \alpha \leq 1 时应选择 r。
那么条件 (1) 的贝叶斯一致性意味着什么呢?它意味着只要可行,参与人 2 在左侧的非平凡信息集中的信念应当基于参与人 1 的策略(尤其是在根节点所选择的行动)利用贝叶斯公式计算。例如,当参与人 1 的策略使他首先选择了 A 时,参与人 2 应当相信该策略并赋予 \alpha=1。反之,当参与人 1 的策略使他首先选择了 B 时,参与人 2 应当赋予 \alpha=0。这是通过条件概率的公式计算的:
\begin{align*} \alpha &= \mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A \mid \text{\small 参与人\ 1\ 选择了\ } A \text{\small \ 或\ } B\big] \\ &= \frac{\mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A\big] \times \mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A \text{\small \ 或\ } B \mid \text{\small 参与人\ 1\ 选择了\ } A \big]}{\mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A \text{\small \ 或\ } B\big]} \\ &= \frac{\mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A\big]}{\mathrm{Pr} \big[\text{\small 参与人\ 1\ 选择了\ } A \text{\small \ 或\ } B\big]} \end{align*}
上式的第一行是 \alpha 的定义,第二行中分子的第二项的值为 1。其他概率应该基于参与人 1 的策略计算。因此,如果策略决定参与人 1 选择 A,则 \alpha = 1/1 = 1;如果策略决定他选择 B,则 \alpha = 0/1 = 0。但是,如果策略决定参与人 1 选择 C,则分母中的概率为 0,这说明上面的算式不适用。此时,我们无法确定参与人 2 在他的非平凡信息集中的信念,而通常我们允许任意信念适用这种情况。
下面我们继续完成分析。在已知随机选择后参与人 2 会选择 R 而参与人 1 会选择 a 的前提下,参与人 1 在第一回合选择 C 的期望收益是 8,高于选择 A 或 B 的最大收益 7。因此 C 是参与人 1 在第一回合的最优选择。但是在这种情况下,博弈无法进行到参与人 2 的非平凡信息集,贝叶斯一致性无法附加任何条件。这允许参与人 2 有任意信念,即 0 \leq \alpha \leq 1。但是在给定 \alpha 的基础上,序贯理性依然有效。因此,此博弈拥有两种完美贝叶斯均衡,即 0 \leq \alpha \leq 3/4 时的 (Ca, \ell R) 和 3/4 \leq \alpha \leq 1 时的 (Ca, rR)。这两组策略组合也是子博弈完美均衡,但是现在有参与人 2 的信念支持。
为了说明贝叶斯一致性可以在子博弈完美性的基础上进行更多限制,我们将 Figure 4.1 中 A 和 \ell 对应的收益修改为 (4,3),正如 Figure 4.9 中所示。
可以确认子博弈完美均衡依然是 (Ca, \ell R) 和 (Ca, rR)。此时,理性的参与人 2 在非平凡信息集上不会选择 r,因为 \ell 永远会带来更高的收益,但是子博弈完美均衡却没有排除 r 的选项。而当我们考虑完美贝叶斯均衡时,所有的信念(即任意 \alpha)都会支持 \ell 而非 r:选择 \ell 的期望收益是 3\alpha + 3(1-\alpha) = 3,选择 r 的期望收益是 2\alpha + 0(1-\alpha) = 2\alpha,而 3 > 2\alpha。因此,唯一一种完美贝叶斯均衡是 (Ca, \ell R) 和任意 \alpha 的组合。
最后,让我们再考虑 Figure 4.7。在 Figure 4.10 中我们给参与人 3 的信息集标注了信念 (\alpha, 1-\alpha)。这个例子中有两种方法可以帮助我们找到完美贝叶斯均衡。第一种是给子博弈完美均衡赋予合适的信念,第二种则是用逆向归纳的方式同时决定策略和信念。下面我们解释第二种方法。首先考虑参与人 3。如果他选择 \ell,则期望收益为 1\alpha + 0(1-\alpha) = \alpha;而如果选择 r,则期望收益为 0\alpha + 3(1-\alpha) = 3 - 3\alpha。因此当 3/4 \leq \alpha \leq 1 时 \ell 为最优选择,而当 0 \leq \alpha \leq 3/4 时 r 是最优选择。这是基于序贯理性条件的分析。
现在假定参与人 3 会选择 \ell。此时参与人 2 应当选择 L。而根据贝叶斯一致性的要求,如果参与人 2 选择了 L,则参与人 3 应当相信这一点,因此 \alpha = 1。而 1 > 3/4,因此参与人 3 应当选择 \ell。此处并没有推出矛盾的结果,因此我们可以继续假设参与人 3 选择 \ell,参与人 2 选择 L。至于参与人 1,在以上假设的基础上,他选 A 的期望收益是 3,大于选择 B 的期望收益 2,因此应当选择 A。综上所述,我们找到了一个完美贝叶斯均衡:(A, L, \ell) 和信念 \alpha = 1 的组合。
如果参与人 3 选择了 r,则参与人 2 应当选择 R,对应了 \alpha = 0 < 3/4,这又支持了参与人 3 选择 r。在此基础上,参与人 1 的最优选择是 B,因为其收益 2 高于选择 A 的收益 1。因此,(B, R, r) 和信念 \alpha = 0 的组合也是完美贝叶斯均衡。
注:另一种更加严格的贝叶斯一致性定义了序贯均衡(sequential equilibrium),见原书第十四章。