8 合作博弈的应用

本章内容基于原书第十章。

以 Chapter 7 的 TU-game 为代表的合作博弈模型通常包含以下特征：根据参与人的可选策略信息得到的抽象化描述，这通常体现为参与人或联盟可以获得的收益或者效用；从策略或公平、效率的角度定义的解；如果可能的话还会包括解的公理化结果，例如 Shapley 值可以通过有效性、对称性、公平性等公理的组合进行定义。

在这一章中我们介绍一些合作博弈的应用模型，包括 Section 8.1 中的讨价还价问题，Section 8.2 中的交换经济，Section 8.3 中的匹配问题，以及 Section 8.4 中的房屋置换问题。

8.1 讨价还价问题

Section 1.3.5 中的分配问题是我们见到的讨价还价问题的第一个例子。在 Section 6.7 中，我们在非合作博弈的框架内讨论了讨价还价问题。这一节里我们从合作博弈以及公理化的角度继续探讨这一问题。我们将会看到这两种方法有着让人意外的内在联系。

8.1.1 纳什谈判解

首先定义二人讨价还价问题¹。

¹ 关于 n 人讨价还价问题以及更具一般性的效用不可转移合作博弈（NTU-game）的讨论可以参考原书第二十一章。

Definition 8.1 二人讨价还价问题（bargaining problem）是满足下列条件的二元组 (S, \boldsymbol{d})：

S \subseteq \mathbb{R}^2 是有界闭凸集（bounded, closed, and convex set）²；
\boldsymbol{d} = (d_1, d_2) \in S 满足 \exists \boldsymbol{x} = (x_1, x_2) \in S, x_1 > d_1, x_2 > d_2。

S 称为可行集（feasible set），\boldsymbol{d} 称为分歧点（disagreement point）。

² \mathbb{R}^k 的一个子集如果满足其内部任意两点间的线段也在其内部，则称其为凸集；如果其包含所有边界点，则称其为闭集；如果其内部所有的点的任意坐标都是有限的，则称其为有界集。

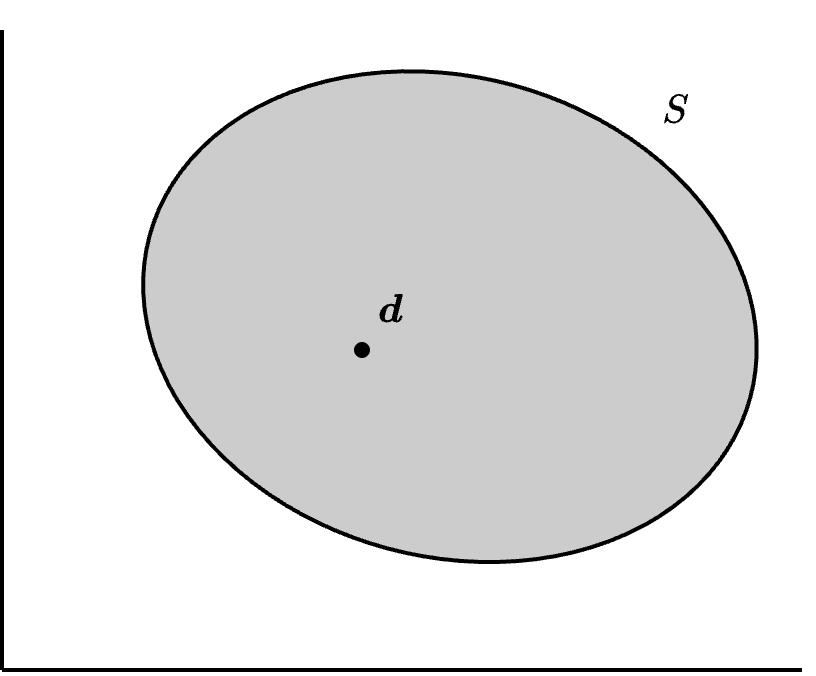
我们可以这样理解讨价还价问题 (S, \boldsymbol{d})：两个参与人针对可行集 S 中的结果进行讨价还价，如果两人都同意 \boldsymbol{x} = (x_1, x_2) \in S，则参与人 1 获得的效用为 x_1，参与人 2 获得 x_2。如果两人没有达成共识，则依照分歧点 \boldsymbol{d} 进行结算，即参与人 1 获得 d_1，参与人 2 获得 d_2，博弈结束。这仅仅是对问题设定的一种解释，并不是对讨价还价过程的实际定义。

在 Section 1.3.5 的例子中，可行集与分歧点的定义是

S = \{\boldsymbol{x} \in \mathbb{R}^2 \mid 0 \leq x_1, x_2 \leq 1, x_2 \leq \sqrt{1-x_1}\}, \quad d_1 = d_2 = 0.

参考 Figure 1.8。一般情况下，S 和 \boldsymbol{d} 的关系类似 Figure 8.1 中所描绘的样子。

Nash, John F. 1950. “The Bargaining Problem.” Econometrica 18 (2): 155. https://doi.org/10.2307/1907266.

我们在 (S, \boldsymbol{d}) 中主要讨论的问题是，双方在哪一点妥协是最好的。这相当于寻找一个函数 F: \mathcal{B} \to \mathbb{R}^2，其中 \mathcal{B} 是所有讨价还价问题的集合。也就是说，F 给每个讨价还价问题 (S, \boldsymbol{d}) \in \mathcal{B} 赋予一个可行点 F(S, \boldsymbol{b})。我们将函数 F 称为（二人）谈判解或议价解（bargaining solution）。根据 Nash (1950)，一个谈判解需要满足四个性质：帕雷托最优性、对称性、标度协变性、以及无关方案独立性。见 Figure 8.2。下面我们分别讨论这四个性质。

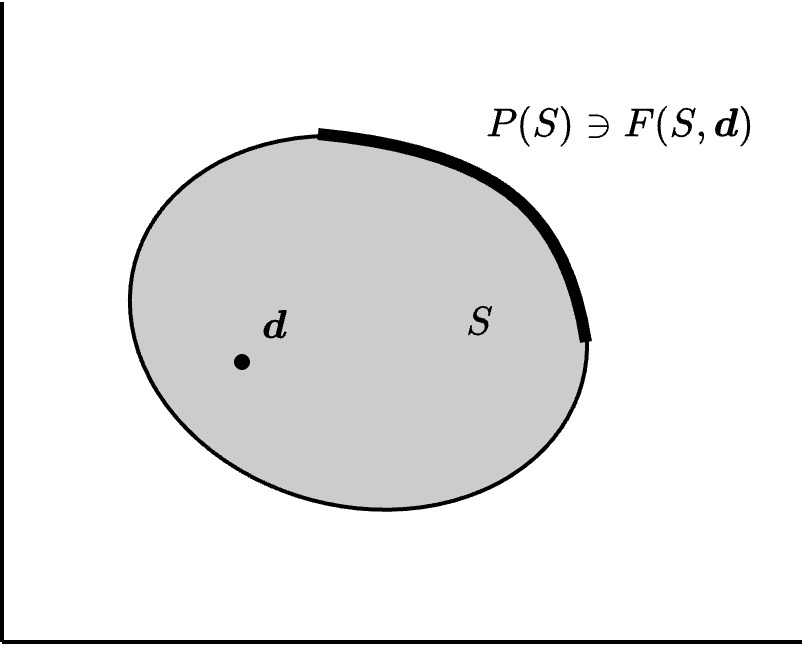
帕雷托最优性（Pareto optimality） 对讨价还价问题 (S, \boldsymbol{d}) \in \mathcal{B}，S 中的帕雷托最优点是那些无法在不减少一个参与人的效用的情况下增加另一个参与人效用的点，即

P(S) = \{\boldsymbol{x} \in S \mid \text{for all }\ \boldsymbol{y} \in S \ \text{ with } \ y_1 \geq x_1, y_2 \geq x_2, \ \text{ we have } \ \boldsymbol{y} = \boldsymbol{x}\}

P(S) 称为 S 的帕雷托最优子集。谈判解 F 如果满足 F(S,\boldsymbol{d}) \in P(S) for all (S,\boldsymbol{d} \in S)，则称 F 为帕雷托最优（Pareto optimal）。帕雷托最优谈判解会给每个讨价还价问题赋予一个帕雷托最优的可行点。见 Figure 8.2 (a)。

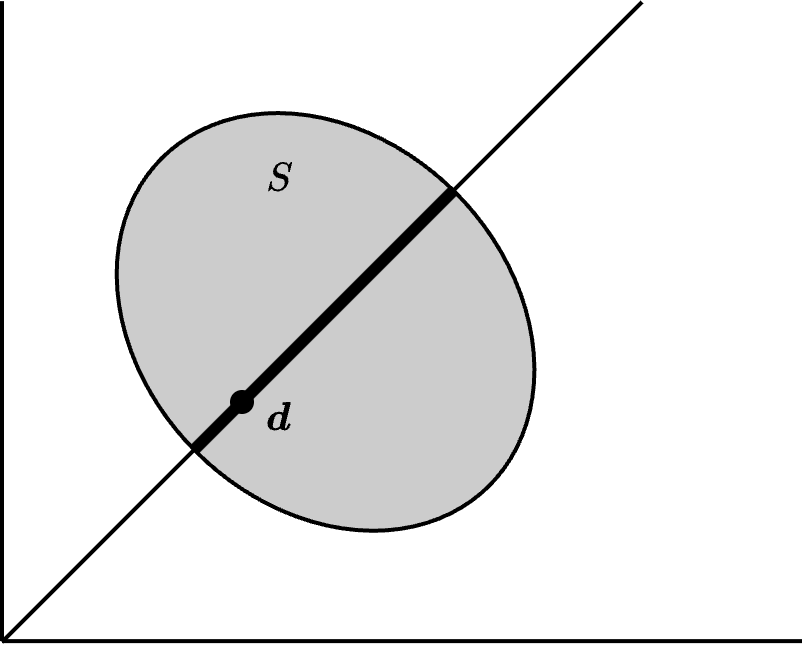
对称性（symmetry） (S, \boldsymbol{d}) \in \mathcal{B} 如果满足 d_1 = d_2 且 S 关于 45^\circ 线对称，即

S = \{(x_2, x_1) \in \mathbb{R}^2 \mid (x_1, x_2) \in S\},

则称 (S, \boldsymbol{d}) 为对称（symmetric）。在对称的讨价还价问题中，除了给参与人人为命名以外，无法通过其他途径区分两个参与人。如果针对每个对称的 (S, \boldsymbol{d}) \in \mathcal{B}，谈判解 F 都满足 F_1(S, \boldsymbol{d}) = F_2(S, \boldsymbol{d})，则 F 也是对称的。因此，一个对称谈判解在对称讨价还价问题中给每个参与人赋予相同的效用。见 Figure 8.2 (b)。

对于对称讨价还价问题 (S, \boldsymbol{d})，满足帕雷托最优性和对称性的谈判解是唯一的，因为 S 中的对称帕雷托最优点只有一个。

标度协变性（scale covariance） 这条性质要求，即使效用的单位发生变化（包括改变坐标系的原点和进行缩放），谈判解也应该保持不变。例如在 Section 1.3.5 的分配问题中，即使我们将效用函数改为 \overline{u}_1 = a_1 \alpha + b_1，\overline{u}_2 = a_2 \sqrt{\alpha} + b_2，a_1, a_2, b_1, b_2 \in \mathbb{R}，a_1, a_2 > 0，对葡萄酒的最终分配结果也不应发生变化。\overline{u}_1 和 \overline{u}_2 可以看作效用函数 u_1 和 u_2 在不同单位下的表达。下面是这一性质的正式表述。谈判解 F 如果对所有 (S, \boldsymbol{d}) \in \mathcal{B}，a_1, a_2, b_1, b_2 \in \mathbb{R}，a_1, a_2 > 0 都满足

F\big(\{\boldsymbol{a}^\top \boldsymbol{x} + \boldsymbol{b} \in \mathbb{R}^2 \mid \boldsymbol{x} \in S\}, \boldsymbol{a}^\top \boldsymbol{d} + \boldsymbol{b}\big) = \boldsymbol{a}^\top F(S, \boldsymbol{d}) + \boldsymbol{b}, \quad \boldsymbol{a} = \begin{pmatrix} a_1 \\ a_2\end{pmatrix}, \boldsymbol{b} = \begin{pmatrix} b_1 \\ b_2\end{pmatrix}

则称 F 为标度协变（scale covariant）。Figure 8.2 (c) 展示了一个简单的例子。

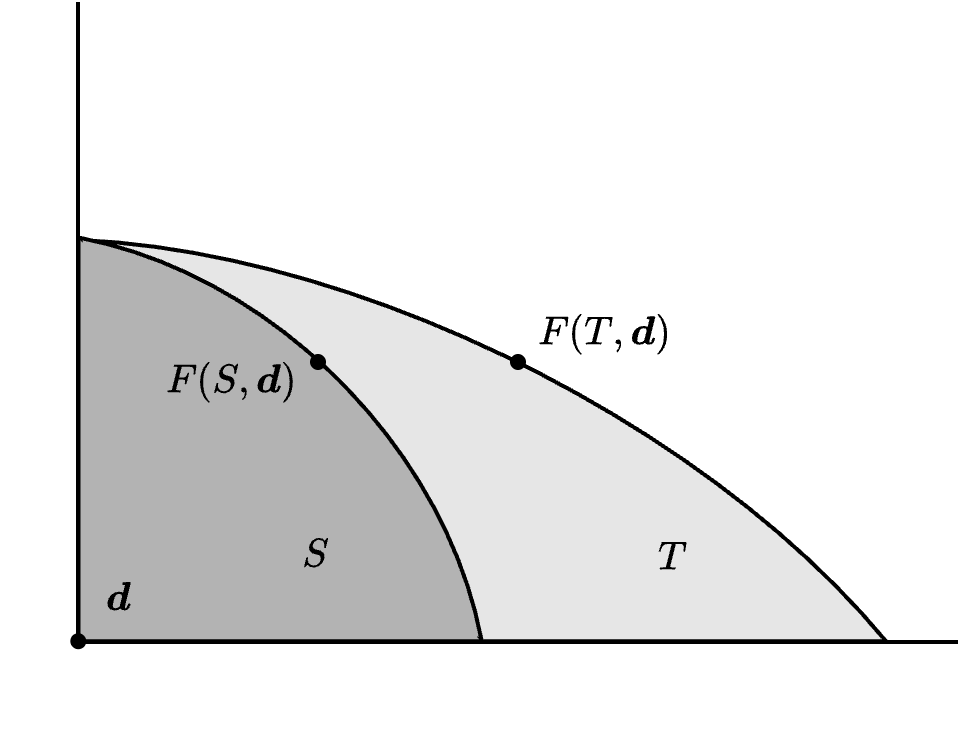
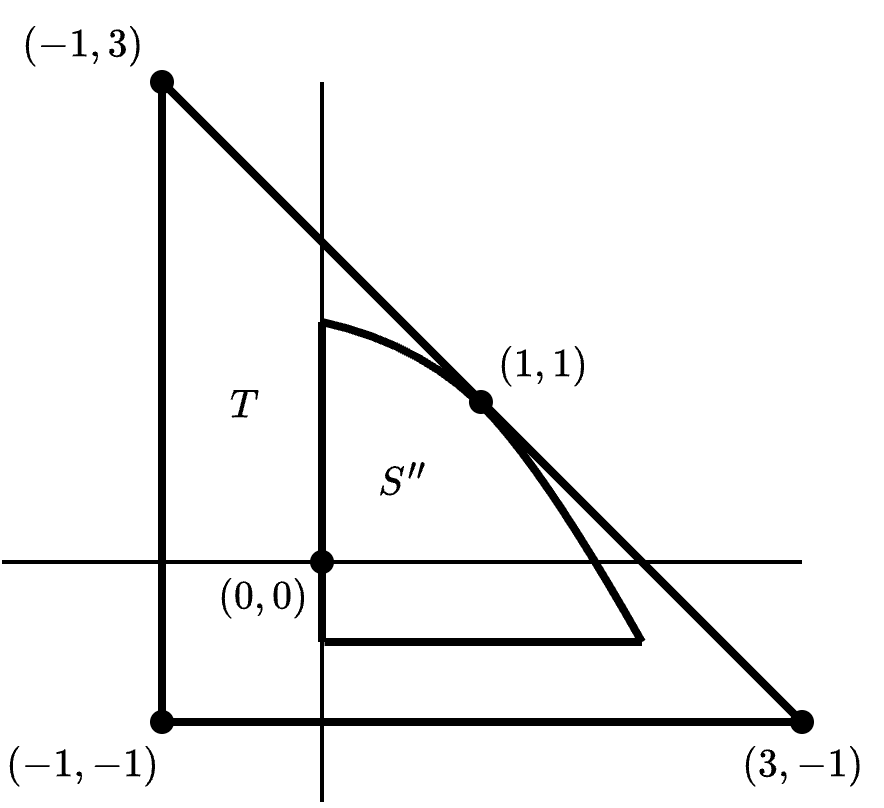
无关方案独立性（independence of irrelevant alternatives, IIA） 这是四个性质中最具争议的一个。假设一个讨价还价问题 (S, \boldsymbol{d}) 的最终分配是 \boldsymbol{z} = F(S, \boldsymbol{d}) \in S。它可以理解为 F 在 S 中找出的最佳妥协点。如果现在有一个更小的讨价还价问题 (T, \boldsymbol{d}), T \subseteq S 满足 \boldsymbol{z} \in T，那么 \boldsymbol{z} 也应该是 T 中的最佳妥协点，因为 T 是 S 的子集，且 T 包含 \boldsymbol{z}。因此，我们的结论应该是 F(T, \boldsymbol{d}) = \boldsymbol{z} = F(S, \boldsymbol{d})。例如在葡萄酒分配问题中，假设最终分配方案是两人平分一升酒，对应效用 (1/2, \sqrt{1/2})。现在假设两人各自最多只能喝 3/4 升酒，喝更多不会带来更大的效用。这时新的可行集是

\textstyle T = \{\boldsymbol{x} \in \mathbb{R}^2 \mid 0 \leq x_1 \leq 3/4, \ 0 \leq x_2 \leq \sqrt{3/4}, \ x_2 \leq \sqrt{1-x_1}\}.

根据前面的逻辑，此时两人依然应该平分，因为 T \subseteq S 且 (1/2, \sqrt{1/2}) \in T。这看上去很有道理，但是其实可以很容易地找到至少存在讨论余地的其他例子。例如，假设参与人 1 依然觉得喝得越多越好，但参与人 2 最多只想喝 1/2 升。这时的可行集是

\textstyle T' = \{\boldsymbol{x} \in \mathbb{R}^2 \mid 0 \leq x_1 \leq 1, \ 0 \leq x_2 \leq \sqrt{1/2}, \ x_2 \leq \sqrt{1-x_1}\},

而结果依然是保持平分。但这时参与人 2 获得了他可以获得的最大效用，只有参与人 1 做出了让步，这看上去也并不是那么的合理。

谈判解 F 如果对 (S, \boldsymbol{d}), (T, \boldsymbol{d}) \in \mathcal{B}，T \subseteq S，F(S, \boldsymbol{d}) \in T 满足 F(T, \boldsymbol{d}) = F(S, \boldsymbol{d})，则称其独立于其他无关方案（independent of irrelevant alternatives）。见 Figure 8.2 (d)。

Definition 8.2 讨价还价问题 (S,\boldsymbol{d}) \in \mathcal{B} 的纳什谈判解（Nash bargaining solution）F^\text{Nash}(S, \boldsymbol{d}) 对应 S 中满足下列条件的唯一点 \boldsymbol{z} \in S：

\boldsymbol{z} = \underset{\boldsymbol{x} \in S, \ x_1 \geq d_1, \ x_2 \geq d_2}{\text{argmax}} \ (x_1 - d_1)(x_2 - d_2)

Theorem 8.1 纳什谈判解 F^\text{Nash} 是唯一同时满足帕雷托最优性、对称性、标度协变性、无关方案独立性的谈判解。

对 Theorem 8.1 的证明感兴趣的同学可以参考原书第二十一章。

Example 8.1 这里我们通过例子展示 Theorem 8.1 中每个条件起到的作用。这也是将证明的思路放在例子中进行展示。令 S = \{(x_1, x_2) \in \mathbb{R}^2 \mid 0 \leq x_1 \leq 2, \ 0 \leq x_2 \leq 4 - x_1^2\}，\boldsymbol{d} = (0,1)。纳什谈判解是 \mathrm{argmax}_{\ 0\leq x_1 \leq 2} \ x_1 (3-x_1^2) 的解，即 (1, 3)。如果我们从第二坐标中减去 1，可以获得新的讨价还价问题

S' = \{(x_1, x_2) \in \mathbb{R}^2 \mid 0 \leq x_1 \leq 2, \ -1 \leq x_2 \leq 3 - x_1^2\}, \quad \boldsymbol{d}' = (0,0)

如果继续将第二坐标除以 2，则可以获得

S'' = \Big\{(x_1, x_2) \in \mathbb{R}^2 \mid 0 \leq x_1 \leq 2, \ -\frac{1}{2} \leq x_2 \leq \frac{3}{2} - \frac{x_1^2}{2}\Big\}, \quad \boldsymbol{d}'' = (0,0)

S'' 的帕雷托最优边界是 f(x_1) = \frac{3}{2} - \frac{1}{2}x_1^2, 0 \leq x_1 \leq 2。此函数在 x_1 = 1 时的导函数值是 -1，也就是说 S'' 在点 (1,1) 的切线的斜率是 -1。现在考虑由三点 (-1,-1), (3,-1), (-1,3) 为顶点的三角形区域组成的可行集 T，见 Figure 8.3。讨价还价问题 (T, (0,0)) 是对称的，根据对称性和帕雷托最优性，(T, (0,0)) 的纳什谈判解是 (1,1)。这一点在 S'' 内部，且 S'' \subseteq T，根据 IIA，(S'', (0,0)) 的纳什谈判解也是 (1,1)。根据 scale covariance，可得 (S', (0,0)) 的纳什谈判解是 (1,2)，同理可得 (S, (0,1)) 的纳什谈判解是 (1,3)。这里我们仅用 Theorem 8.1 中的性质就解出了纳什谈判解，并且与利用定义公式的计算结果相同。

8.1.2 与鲁宾斯坦序贯议价模型的关系

在 Section 6.7.2 中我们学习了（无限回合）鲁宾斯坦序贯议价模型，其中参与人通过交替报价的方式尝试达成共识。下面我们以 Section 1.3.5 的分配问题为例考察鲁宾斯坦模型和纳什谈判解之间的关系。

这个问题的纳什谈判解是 (2/3, \sqrt{1/3})，这意味着参与人 1 分得 2/3 升葡萄酒，参与人 2 分得 1/3 升。而在鲁宾斯坦的无限回合模型（折现因子 0 < \delta < 1）中，子博弈完美均衡策略是参与人 1 提议 \boldsymbol{x} = (x_1, x_2) \in P(S)，参与人 2 提议 \boldsymbol{y} = (y_1, y_2) \in P(S)，且满足

x_2 = \delta y_2, \quad y_1 = \delta x_1.

由此可得

\sqrt{1-x_1} = x_2 = \delta y_2 = \delta \sqrt{1-y_1} = \delta \sqrt{1-\delta x_1}

进而推出 1-x_1 = \delta^2 (1-\delta x_1)，解之可得

x_1 = \frac{1-\delta^2}{1-\delta^3} = \frac{1+\delta}{1+\delta+\delta^2}.

如果我们令 \delta 趋近于 1，则 x_1 的极限是

\lim_{\delta \to 1} \frac{1+\delta}{1+\delta+\delta^2} = \frac{2}{3},

和参与人 1 在纳什谈判解中获得的效用一致。这并不是巧合，从 x_2 = \delta y_2 和 y_1 = \delta x_1 可得

(x_1 - d_1)(x_2 - d_2) = x_1 x_2 = (y_1 / \delta)(\delta y_2) = y_1 y_2 = (y_1 - d_1)(y_2 - d_2)

也就是说，鲁宾斯坦模型的均衡中的提议 \boldsymbol{x} 和 \boldsymbol{y} 的“纳什积”相等。Figure 8.4 中画出了 \delta = 0.5 时的两个提议点的位置。

Figure 8.4: 葡萄酒分配问题。分歧点是原点，\boldsymbol{z} 是纳什谈判解。点 \boldsymbol{x} 和 \boldsymbol{y} 分别是 \delta = 0.5 的鲁宾斯坦模型中参与人 1 和 2 在子博弈完美均衡中的提议。

所以，鲁宾斯坦无限回合序贯议价模型的子博弈完美均衡收益在折现因子趋近于 1 时的极限值和纳什谈判解的分配结果相同。

Example 8.2 在 Example 8.1 中，讨价还价问题 (S',(0,0)) 对应的鲁宾斯坦模型的均衡提议可以通过下面的方程组计算

x_2 = \delta y_2, \quad y_1 = \delta x_1, \quad x_2 = 3 - x_1^2, \quad y_2 = 3 - y_1^2

经计算可得

x_1 = \sqrt{\frac{3(1-\delta)}{1-\delta^3}} = \sqrt{\frac{3}{1+\delta+\delta^2}}.

当 \delta \to 1 时，

\lim_{\delta \to 1} \sqrt{\frac{3}{1+\delta+\delta^2}} = 1, 这也是参与人 1 的纳什均衡解分配。

8.2 交换经济

这里省略这一节的内容，请参考原书第十章第二节。

8.3 匹配问题

匹配问题泛指参与人之间需要进行两两配对的问题，例如学生和学校、医院和医生、员工和企业、有结婚意愿的男女等。这些例子里有的一对多匹配，有的是一对一匹配。这一节中我们讨论一对一匹配。

假设参与人可以分成人数相同的两个组（人数为有限且非空），分别记作 M 和 W。每个 M 中的参与人都对 W 中他认为可以在一起的参与人持有严格偏好（意味着和其他 W 中的参与人在一起还不如保持单身），同样，每个 W 中的参与人都对 M 中她认为可以在一起的参与人持有严格偏好。在这个问题中，匹配（matching）指的是给每个 M 中的参与人指定最多一个 W 中的参与人，同时给每个 W 中的参与人指定最多一个 M 中的参与人。因此这是一个一对一的映射关系，也就是说不会给两个及以上 M 中的参与人指定同一个 W 中的参与人，反之亦然。

这个匹配问题也可以称为结婚问题（marriage problem），M 和 W 分别代表男性和女性。但这仅仅是为了叙事上的方便，同样的设定也可以应用在房间和住户间的匹配等类似问题上。

让我们首先考虑 Table 8.1 中的例子。这里男性集合为 M = \{m_1, m_2, m_3\}，女性集合为 W = \{w_1, w_2, w_3\}。每一列给出了一个参与人的偏好。例如 m_1 喜欢 w_2 超过 w_1，喜欢 w_1 超过保持单身，喜欢保持单身超过 w_3。一个匹配的例子是 (m_1, w_1), (m_3, w_2), m_2, w_3，意味着 m_1 和 w_1 结婚，m_3 和 w_2 结婚，m_2 和 w_3 各自保持单身³。这个匹配并不稳定（stable），因为 m_1 和 w_2 更偏好和彼此结婚而不是和匹配中的另一方结婚，同时 m_2 和 w_3 也更偏好和彼此结婚而不是各自保持单身。同理，所有包含 (m_1, w_3) 的匹配都不稳定，因为相比和 w_3 结婚，m_1 更偏好保持单身。

³ 这个问题中一共有 34 种不同的匹配。

Table 8.1: 一个匹配问题

参与人	m_1	m_2	m_3	w_1	w_2	w_3
第一偏好	w_2	w_1	w_1	m_1	m_2	m_1
第二偏好	w_1	w_2	w_2	m_3	m_1	m_3
第三偏好		w_3		m_2	m_3	m_2

为了排除不稳定匹配，一个显而易见的方法是寻找匹配问题的核。一个匹配中如果不存在能够通过不服从匹配（包括结婚和保持单身）而产生更好结果的参与人（联盟），那么该匹配就包含在核中。下面是核匹配的两个必要条件：

跟保持单身相比，每个参与人都更偏好和匹配中指定的人结婚；
如果 m \in M 和 w \in W 没有被匹配成一对，则以下情况不会同时出现：
- m 更偏好和 w 结婚（无论他被指定和其他人结婚或者保持单身），
- w 更偏好和 m 结婚（无论她被指定和其他人结婚或者保持单身）。

如果不符合第一条，则该参与人可以通过离婚让自己更加满足；如果不符合第二条，则 m 和 w 可以通过和彼此结婚让各自都更加满足。因此，符合这两个条件的匹配称为稳定匹配。在核中的匹配都是稳定匹配，并且任何稳定匹配都包含在核中。为了证明后半句（即这两个条件也是充分条件），我们可以假设一个不在核中的匹配符合这两个条件，此时就存在一个参与人联盟，使该联盟内的参与人通过相互结婚或者保持单身而更加满足。如果通过保持单身而变得更好，则不符合条件一；如果联盟里的两个人通过和彼此结婚而变得更好，则不符合条件二。这和假设相矛盾，因此任何稳定匹配都是核匹配。换句话说，匹配问题的核是所有稳定匹配的集合。

那么如何找到稳定匹配呢？常用方法是由 Gale 和 Shapley 提出的延迟接受算法（deferred acceptance algorithm）。在这个算法中，由一组中的参与人进行求婚，另一组中的参与人则决定接受或者拒绝。这里假设让男性求婚。在第一回合，每个男性向他最想结婚的女性求婚（如果他更偏好保持单身则保持单身），每个女性从向自己求婚的男性当中选择自己最偏好的一位（如果更偏好保持单身或没有收到求婚则选择保持单身）。这样可以产生一些配对，我们称之为订婚。在第二回合，之前被拒绝的男性向自己第二偏好的女性求婚（或保持单身），然后每个女性从向自己求婚的男性以及当前订婚的男性中选择自己最偏好的一位。重复这一操作直至所有的求婚都被接受。最后让所有订婚的配对结婚，没有订婚的配对保持单身，从而产生一个匹配。

由延迟接受算法得出的匹配是稳定的。最终保持单身的男性肯定是被所有求婚对象拒绝了，因此没有哪个女性认为和他结婚好于和现在的匹配对象结婚或者保持单身。最终保持单身的女性肯定是没有接到任何她想结婚的男性的求婚。最后考虑 m \in M 和 w \in W 最终各自结婚了但不是和彼此结婚的情况。如果 m 更偏好和 w 结婚而非现在的妻子，则说明 w 在某一回合曾经拒绝 m 的求婚而选择了更好的。如果 w 更偏好和 m 结婚而非现在的丈夫，则说明 m 从未向 w 求过婚，因此 m 更偏好现在的妻子。

如果让女性求婚，延迟接受算法也适用，但通常会得到一个不一样的稳定匹配。

Table 8.2 展示了如何用延迟接受算法解 Table 8.1 中的匹配问题。

Table 8.2: 用延迟接受算法解 Table 8.1 中的匹配问题。最终获得的匹配是 (m_1, w_1), (m_2, w_2), m_3, w_3。

	第一回合	第二回合	第三回合	第四回合
m_1	\to w_2	被拒绝	\to w_1
m_2	\to w_1 被拒绝	\to w_2
m_3	\to w_1		被拒绝	\to w_2 被拒绝

除了通过延迟接受算法获得的稳定匹配，还可能存在其他稳定匹配。而在延迟接受算法中，让男性求婚得到的稳定匹配对于男性来说是最优的，让女性求婚得到的稳定匹配对于女性来说是最优的。

8.4 房屋置换

在房屋置换问题中存在有限多个参与人，每人个参与人拥有一套房子，并且每人都对所有房子有自己的偏好。参与人们可以通过置换房子达到收益最大化。

令参与人集合为 N = \{1,\dots, n\}，每个参与人 i 拥有的房子为 h_i，每个人都对全部 n 个房子持有严格偏好。此问题的核分配会分给每个参与人一套房子，且不存在任何联盟可以通过内部置换初始持有房屋的方式让每一个成员都获得更大的收益⁴。例如，假设一个分配分给参与人 1 h_1，分给参与人 2 h_3。二人如果交换初始持有的房屋，则参与人 1 会获得 h_2，优于他分得的 h_1；参与人 2 会获得 h_1，也优于他分得的 h_3。因此，这个分配方法不会出现在核分配中。

⁴ 这里可以置换的只是初始拥有的房屋，而非执行该分配后获得的房屋。

考虑 Table 8.3 中的例子。这个问题存在六种不同的分配。Table 8.4 列出了这些分配，以及哪些联盟可以通过内部置换进行改善。

Table 8.3: 一个三人房屋置换问题

参与人	1	2	3
第一偏好	h_3	h_1	h_2
第二偏好	h_2	h_2	h_3
第三偏好	h_1	h_3	h_1

Table 8.4: 对 Table 8.3 中问题的分析。这个问题共有两个核分配。

参与人 1	参与人 2	参与人 3	可以进行改善的联盟
h_1	h_2	h_3	\{1,2\}, \{1,2,3\}
h_1	h_3	h_2	\{2\}, \{1,2\}
h_2	h_1	h_3	无：这是核分配
h_2	h_3	h_1	\{2\}, \{3\}, \{2,3\}, \{1,2,3\}
h_3	h_1	h_2	无：这是核分配
h_3	h_2	h_1	\{3\}

对于大型问题（即参与人人数很多的问题），如 Table 8.4 中的穷举法将会变得非常复杂。另一种更加方便的替代方法是 top trading cycle 算法（TTC 算法，根据其含义或可翻译为第一偏好交易环算法）。在房屋置换问题中，一个 top trading cycle 指的是一个参与人序列 i_1, i_2, \dots, i_k，k \geq 1，其中 i_1 最偏好的房屋是 h_{i_2}，i_2 最偏好的房屋是 h_{i_3}，依此类推，最后 i_k 最偏好的房屋是 h_{i_1}。如果 k=1，这意味着参与人 i_1 已经拥有自己最偏好的房屋。在 TTC 算法中，我们尝试寻找一个 top trading cycle，然后将其中每个参与人最偏好的房屋置换给他。随后将这些参与人和他们的房屋从问题中移除，寻找下一个 top trading cycle，然后再进行置换。重复这一过程直至将所有人移除。

对于 Table 8.3 中的问题来说，唯一的 top trading cycle 是 1, 3, 2，对应分配 1: h_3, 3: h_2, 2: h_1。这是一个核分配，因为每个都获得了他最偏好的房子。TTC 算法在严格偏好下总能得到核分配。

那么 Table 8.4 中的另一个核分配 1: h_2, 3: h_3, 2: h_1 呢？在这个分配中，全体联盟可以进行“弱改进”，即通过 1: h_3, 3: h_2, 2: h_1 使参与人 1 和 3 都获得更想得到的房子，参与人 2 也没有变得更差。我们称所有无法进行弱改进的分配集合为“强核”（strong core）。即在强核分配中，没有任何联盟可以让其成员不会变得更差，但能让至少一个成员变得更好。在这个例子里，1: h_3, 3: h_2, 2: h_1 是唯一的强核分配。事实上，对于严格偏好房屋置换问题，TTC 算法给出的分配是唯一的强核分配。